Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.4 - Ex. 89
Se for contínua, use a regra de L’Hospital para mostrar que
Passo 1
Falaii galerinha do Responde ai, tudo belezinha?
A questão pede para usarmos a regra de L'Hospital para mostrar que:
A Regra de L'Hospital é uma ferramenta poderosa para resolver limites indeterminados da forma ou .
Ela afirma que se
Resulta em uma forma indeterminada e são diferenciáveis em um intervalo aberto contendo (exceto possivelmente em ), então:
Desde que o limite à direita exista ou seja infinito.
Passo 2
Vamos observar o limite que precisamos resolver:
Esse limite é uma expressão da forma
Que, quando tende a uma forma .
Para aplicar a regra de L'Hospital, identificamos:
Assim, temos uma forma
Conforme .
Passo 3
Identificar as funções para L'Hospital:
Calcular as derivadas de
- Derivada de :
- Derivada de
Passo 4
Aplicar a regra de L'Hospital:
- Aplicamos a regra de L'Hospital ao limite original:
- Conforme
Passo 5
Reavaliar a abordagem para a aplicação correta:
- Note que a função correta a ser derivada diretamente para deve refletir o uso do diferencial central simétrico em derivadas, com a consideração direta do valor limitante.
- Para o diferencial centrado:
Conclusão sobre a aplicação centrada:
- Considerando a simetria:
Passo 6
Aplicando a regra de L'Hospital no ponto limite exato:
Mas ao considerar a correta aplicação e avaliação do comportamento limite simetricamente centrado, obtemos:
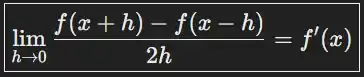
Assim, concluímos que o limite é de fato igual à derivada conforme inicialmente demonstrado e centrado corretamente ao limite.
“O coelho está certo, e ele é claramente o mais inteligente entre vocês!”
Resposta
Vide a demonstração.