Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 1.2 - Ex. 2

Siga as instruções do problema 1 para os problemas de valor inicial a seguir

(a) d y d t =   y - 5   ,       y 0 = y 0

(b) d y d t =   2 y - 5   ,       y 0 = y 0

(c) d y d t =   2 y - 10   ,       y 0 = y 0

Passo 1

Vamos agora ver como resolvemos edo do seguinte tipo:

d y d t = a y - b

Sabemos que y é função de t, portanto multiplicamos ambos os lados da equação por d t .

d y = a y - b d t ⇒ d y y - b a = a d t   c o m   a ≠ 0

Agora, integramos ambos os lados

∫ d y y - b a = ∫ a d t ⇒ ln ⁡ y - b a = a t + C  

⇒ y = c e a t + b a

Repara que para c = 0, temos a solução de equilíbrio.

Caso tenhamos um valor inicial podemos descobrir a constante da solução, por exemplo:

Seja y 0 = y 0

⇒ y 0 = c e a 0 + b a ⇒ c = y 0 - b a

Passo 2

Utilizando do passo 1 para resolver as letras a,b e c, segue que:

(a) d y d t =   y - 5   ,       y 0 = y 0

y   = y 0 - b a e a t + b a ⇒   y 0 - 5 e t + 5

(b) d y d t =   2 y - 5   ,       y 0 = y 0

y   = y 0 - b a e a t + b a ⇒   y 0 - 5 2 e 2 t + 5 2

(c) d y d t =   2 y - 10   ,       y 0 = y 0

y   = y 0 - b a e a t + b a ⇒   y 0 - 5 e 2 t + 5

Passo 3

a)

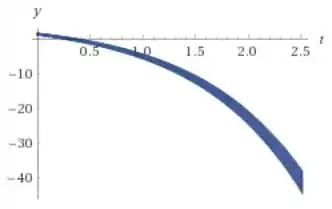
b)

c)

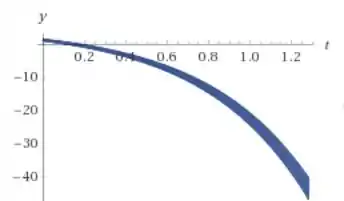
Resposta

A posição de equilíbrio é 5 para as letras (a) e (c) e 5/2 para a letra b, vemos pelos gráfico que a solução se afasta do equilíbrio mais rápido em (b) e (c) do que em (a)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva.(d y)/(d x) = e^(- y)
Resolva.(d x)/(d t) = ln t
Resolva.(d T)/(d t) = - 2 (T - 10)
Resolva.(d v)/(d t) = v^2 - v
Obtenha um campo de direção e o adicione aos gráficos das curvas integrais que passam pelos pontos dados. y ' = y ( 0,1 ) ( 0,2 ) 0 , - 1