Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.6 - Ex. 35
Se
Encontre . Verifique que sua resposta é razoável comparando os gráfico de .
Passo 1
Fala galera, nessa questão temos a seguinte função
E queremos calcular a sua derivada.
Para isso precisamos saber a derivada da função seno e da função logaritmo natural, e depois é só soma-las, pois pela propriedade da soma, a derivada da soma de funções é a soma das derivadas.
Depois, vamos plotar os gráficos de e (sua derivada) para ver se nossa resposta é razoável.
Passo 2
Calculando e utilizando a propriedade da soma, temos que
Passo 3
Agora, esboçando os gráficos, onde a curva em vermelho representa e a curva em azul
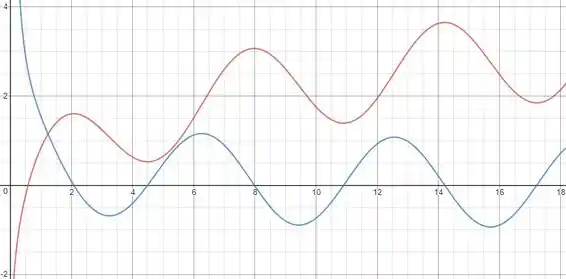
Podemos concluir que a curva de é razoável, pois aumenta quando apresenta valores positivos e diminui quando apresenta valores negativos.
E quando apresenta uma reta tangente horizontal, vale zero.
Resposta
Os gráficos são razoáveis.