Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.8 - Ex. 26
(a) Se seu sistema de computação algébrica traça o gráfico de curvas definidas implicitamente, use-o para estimar os valores mínimo e máximo de sujeita a por métodos gráficos.
(b) Resolva o problema da parte (a) com o auxílio dos multiplicadores de Lagrange. Use um SCA para resolver as equações numericamente. Compare sua resposta com a da parte (a).
Passo 1
Oie, tudo bem? Vou te ajudar a resolver essa atividade. A gente vai precisar utilizar o um software aqui.
Inicialmente iremos traçar o gráfico da função:
E em conjunto iremos traçar o gráfico da sua restrição:
A partir disso iremos observar os máximos e mínimos da função. Aqui iremos utilizar o GeoGebra, ele é gratuito e fácil de utilizar, além de ser online.
Já para a letra b), para usar os multiplicadores de Lagrange, a gente utiliza a igualdade:
Em que é o gradiente e é dado por:
Para derivar parcialmente devemos derivar em relação a uma variável e considerar todas as outras com constantes.
Com isso em mãos, a gente encontra os valores de e resolvendo os sistemas com a equação da restrição. Iremos então encontrar um ponto crítico que deve ser testado na função .
Passo 2
(a) Usando um SCA, vamos traçar as curvas, iremos plotar para diferentes valores de .
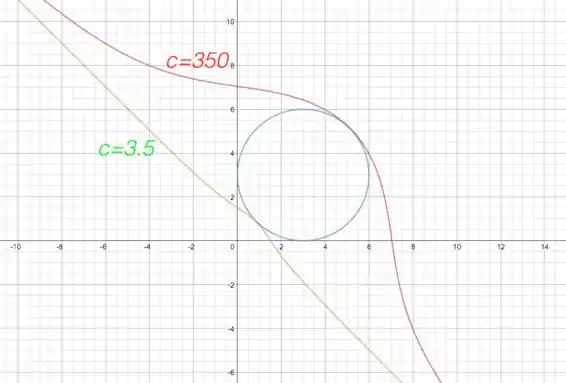
Os gráficos de e parecem ser tangentes à circunferência. Então, seria o mínimo, e seria o máximo, fazendo uma estimativa.
Passo 3
(b) Para usar multiplicadores de Lagrange, devemos ter:
Sendo que:
E
Vamos derivar parcialmente para encontrarmos os gradientes:
E para :
Temos então a nossa igualdade:
Então ficamos com três equações:
Passo 4
Vamos gerar um código python para resolver essas equações:
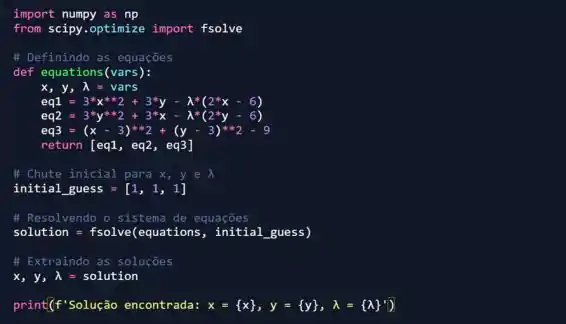
Vamos ter então:
Substituindo na função, encontramos os valores de máximos e mínimos:
Ou seja, o mínimo e o máximo calculados estão de acordo com os estimados no item (a).
Resposta
(a) e
(b) e