Exercícios de Multiplicadores de Lagrange com 1 Restrição - Lista de Exercícios Resolvida
Questão 2
Considere a função
(a) Determine e classifique os pontos críticos de em todo o .
(b) Determine os pontos de máximo e mínimo de sobre a circunferência:
(c) Determine os valores máximo e mínimo de no disco
e os pontos onde estes valores ocorrem.
Ver solução completaQuestão 4
Considere a função definida por
(a) Determine os pontos críticos de e classifique-os.
(b) Determine os pontos de máximo e mínimo absolutos de no conjunto
Ver solução completaQuestão 6
A temperatura em uma placa de metal é dada por
- Determine e classifique os pontos críticos de em todo .
- Determine os pontos onde ocorrem a maior e a menor temperatura na região
Questão 7
Deseja-se construir uma caixa retangular de de volume. O custo do material a ser utilizado é de por para a tampa e para o fundo, por para um par de lados opostos e por para o outro par de lados opostos. Determine as dimensões da caixa que minimizem o custo.
Ver solução completaQuestão 9
Ache o volume máximo do paralelepípedo no primeiro octante inscrível no elipsóide
Ver solução completaQuestão 10
Considere a função dada por
para um real fixado.
a) Determine os pontos críticos de e classifique-os, em função do parâmetro .
b) Faça e determine o valor máximo e o valor mínimo de em
Ver solução completaQuestão 11
Desejamos fabricar um cilindro circular reto de raio e altura . Usando o método dos multiplicadores de Lagrange, encontre o volume máximo do cilindro quando sua área (incluindo as duas tampas) é de unidades de área.
Dica: Lembre que a área lateral de um cilindro circular reto de raio e altura é , e o volume é .
Ver solução completaQuestão 12
Dada a função
Determine os pontos de máximo e mínimo absolutos de na região
Ver solução completaQuestão 14
Determine, se existirem, os pontos de máximo e mínimo absolutos de no domínio .
Ver solução completaQuestão 15
Dada a função ,
- Classifique os pontos críticos de .
- Determine os valores de máximo e de mínimo de no compacto
Questão 16
Justifique a existência e determine os pontos de máximo e mínimo de
em
Ver solução completaQuestão 17
Considere a função dada por
para um real fixado.
a) Determine os pontos críticos de e classifique-os, em função do parâmetro .
b) Faça e determine o valor máximo e o valor mínimo de em
Ver solução completaQuestão 19
Determine a equação do plano tangente à superfície , com e maiores do que , que forma um tetraedro mínimo com os planos coordenados.
Dica: O volume do tetraedro formado pelos planos coordenados e pelo plano no primeiro octante é dado por .
Ver solução completaQuestão 21
Foi construída uma caixa com tampa, na forma de um paralelepípedo e com de volume. O material a ser utilizado nas laterais custa o dobro em relação ao que será utilizado na superfície do fundo. De acordo com sua resolução as dimensões da caixa que minimizam o custo do material são:
; ;
; ;
; ;
; ;
Ver solução completaQuestão 22
Calcule o valor máximo e o valor mínimo da função
Restrita a porção do plano
Usando obrigatoriamente o método dos multiplicadores de Lagrange.
Ver solução completaQuestão 23
Deseja-se encontrar os pontos de máximo e mínimo de sobre o conjunto .
- O problema tem solução? Justifique.
- Em caso afirmativo, determine tais pontos.
- A função acima tem ponto de máximo sobre o conjunto ? E de mínimo? Justifique suas respostas.
Questão 25
Maximize sujeito a , onde é uma constante real positiva fixa. Qual é o valor máximo da função objetivo no conjunto determinado pela restrição?
Mostre que para todo ocorre
Ver solução completaQuestão 26
34. Obtenha o ponto da elipse situado no 1° quadrante, no qual a tangente à curva forma com os eixos coordenados o triângulo de menor área possível. Calcule essa área mínima.
Ver solução completaQuestão 27
Um disco circular tem a forma da região . Se graus é a temperatura em qualquer ponto do disco e , encontre os pontos mais quentes e mais frios do disco.
Ver solução completaQuestão 28
23. Encontre os extremantes da função objetivo no conjunto admissível (conjunto que satisfaz a restrição). Encontre também, se houver, os extremantes de em .
, sujeito à .
Ver solução completaQuestão 29
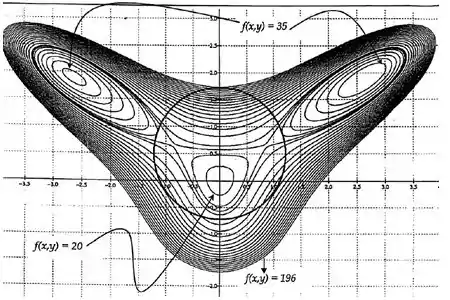
Considere a figura abaixo que representa as curvas de nível de uma função com derivadas parciais contínuas e uma restrição . (Circunferência)
a) Marque na figura todos os pontos críticos de .
b) Tendo por base o valor das curvas de nível indicado na figura classifique os pontos críticos em a)
c) Desenhe na figura o vetor gradiente da função no ponto
d) Indique, com um X sobre a figura, os pontos que são solução do seguinte sistema:
e) Olhando para a figura, você consegue concluir onde ocorrem os valores máximo e mínimo da função restrita à circunferência?
Questão 30
Uma empresa de serviço de entrega restringe as dimensões do pacote a caixas retangulares tais que o comprimento mais o dobro da largura mais o dobro da altura não pode exceder 108 centímetros. Quais são as dimensões do pacote com maior volume que a empresa entrega?
Ver solução completaQuestão 31
Encontre os valores extremos da função na região definida pela desigualdade .
Ver solução completaQuestão 32
Considere a função
- Determine e classifique os pontos críticos de em todo
- Determine os pontos de máximo e mínimo de sobre a circunferência:
- Determine os valores máximos e mínimos de no disco e os pontos onde esses valores ocorrem
Questão 33
Considere a função
(a) Determine e classifique os pontos críticos de em todo o .
(b) Determine os pontos de máximo e mínimo de sobre a circunferência:
(c) Determine os valores máximo e mínimo de no disco
e os pontos onde estes valores ocorrem.
Ver solução completaQuestão 34
Deseja-se construir uma caixa retangular de de volume. O custo do material a ser utilizado é de por para a tampa e para o fundo, por para um par de lados opostos e por para o outro par de lados opostos. Determine as dimensões da caixa que minimizem o custo.
Ver solução completaQuestão 35
Determine os valores máximos e mínimos absolutos da função no conjunto
Ver solução completaQuestão 36
12 - Determine os valores máximo e mínimo, se existirem, da função sujeita aos vínculos e .
Ver solução completaQuestão 37
Use o método dos multiplicadores de Lagrange para determinar o valor máximo da função
Com a restrição
Conclua que
Ver solução completaQuestão 38
A soma das coordenadas do ponto da superfície
Pertencente ao semiespaço superior e mais próximo da origem é:
Questão 39
Verifique que entre todos os triângulos, aquele cujo produto dos senos de seus ângulos internos é máximo, é o triângulo equilátero.
Lembrete: A soma dos ângulos internos de um triangulo é
Ver solução completaQuestão 41
Determine os valores máximo e mínimo absolutos de na região descrita pela desigualdade
Ver solução completaQuestão 42
Seja
Seja
Com .
Encontre os valores de máximos e mínimos globais de em .
Ver solução completaQuestão 43
Considere a função
Definida no conjunto
Assinale a afirmativa correta:
- em dois pontos de máximo e nenhum ponto de mínimo absoluto em . O valor máximo de em é .
- em dois pontos de máximo e um ponto de mínimo absoluto em . O valor máximo e mínimo de em são e , respectivamente.
- em dois pontos de máximo e dois pontos de mínimo absolutos em . O valor máximo e mínimo de em são e , respectivamente.
- não tem pontos de máximo e mínimo absoluto em
- Todas as demais alternativas são falsas.
Questão 44
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita a restrição dada:
Ver solução completaQuestão 45
Utilize os multiplicadores de Lagrange para determinar a menor distância entre o ponto e o plano
Ver solução completaQuestão 46
A soma das coordenadas do ponto da superfície
Pertencente ao semiespaço superior e mais próximo da origem é:
Questão 47
Considere
- Exiba todos os pontos críticos de e explicite o gradiente de .
- Classifique os pontos críticos de e explicite a matriz hessiana de
- Seja
- Seja
Determine o valor máximo e o valor mínimo de restrita à .
Determine o valor máximo global e o valor mínimo global de restrita a . Explicite os pontos onde o máximo e mínimo são assumidos e diga se são pontos do interior ou da fronteira de .
Ver solução completaQuestão 48
A soma das coordenadas do ponto da superfície
Pertencente ao semiespaço superior e mais próximo da origem é:
Questão 49
Determine o retângulo de perímetro máximo (com lados paralelos aos eixos coordenados) que pode ser inscrito na elipse de equação
Ver solução completaQuestão 50
O valor mínimo absoluto da função na região é:
- Nenhuma das demais alternativas
Questão 51
O plano intercepta o paraboloide em uma elipse. Determine os pontos da elipse que estão mais próximos e mais longe da origem.
Ver solução completaQuestão 52
Deseja fabricar-se uma caixa de papelão retangular, sem tampa, com volume . Quais as dimensões da caixa que minimizam a quantidade de papelão a ser utilizado?
80
Ver solução completa
Questão 53
Seja o gráfico da função
a) Exiba um ponto , ta que o plano tangente à neste ponto é paralelo ao plano dado por
b) Seja
i) Determine os pontos dp traço de onde a reta tangente é vertical, isto é, paralela ao eixo
ii) Exiba a parametrização da curva
tal que o traço de está contigo no gráfico (superfície ) e a projeção ortogonal de no plano é a curva . Explicite e calcula
iii) Escreva o vetor velocidade da curva em e exiba a equação paramétrica da reta tangente à em
Ver solução completaQuestão 54
Seja .
a) Exiba a matriz hessiana de no ponto e a aproximação quadrática de neste ponto.
b) Encontre um aberto tal que a matriz hessiana de em todo ponto seja estritamente positiva definida. Desenhe o aberto e, ao lado, sua fronteira.
c) Encontre um aberto tal que a matriz hessiana de em todo ponto seja indefinida.
d) Classifique os pontos críticos de .
e) Calcule o valor de máximo de restrita à curva
Dica: Considere que
Ver solução completaQuestão 56
Seja uma constante real. Calcule o valor máximo e o valor mínimo da função
na esfera
Ver solução completaQuestão 57
Quais os valores mínimos e máximos respectivamente de no domínio ?
e ;
e ;
e ;
e ;
e .
Ver solução completaQuestão 58
A temperatura em uma placa de metal é dada por
- Determine e classifique os pontos críticos de em todo .
- Determine os pontos onde ocorrem a maior e a menor temperatura na região
Questão 59
Três alelos (versões alternativas de um gene) A, B e O determinam os quatro tipos de sangue: , , , e . A Lei de Hardy-Weinberg afirma que a proporção de indivíduos em uma população que carregam dois alelos diferentes é , em que e são as proporções de , e na população. Sabendo que , determine a proporção máxima de indivíduos que carregam dois alelos em uma população.
Ver solução completaQuestão 61
4. A temperatura em um ambiente com solo plano não depende da altura. Fixando no solo uma origem, o eixo apontando para leste e o eixo para norte, ela é dada por
- Use multiplicadores de Lagrange para encontrar dentre os pontos que distam da origem, os de temperatura máximo e mínima?
Questão 62
Utilize o método de multiplicadores de Lagrange para determinar os valores extremos da função
Sobre a esfera
E classifique-os como máximo ou mínimo.
Ver solução completaQuestão 63
6. Determinar os pontos de máximos e/ou mínimos da função dada, sujeita às restrições indicadas:
d) ; com a condição de que .
Ver solução completaQuestão 64
7. Encontre os valores máximo e mínimo da função sujeita a restrição .
Ver solução completaQuestão 65
Tres números positivos satisfazem a relação
O maior valor possível para o produto é:
- 4000
- 5000
- 2000
- 1000
- 1024
Questão 66
Um fio de coprimento deve ser dividido em partes. Determine o comprimento de cada parte de modo que o produto dos comprimentos das partes seja máximo.
Ver solução completaQuestão 69
(Capítulo 14.8 – Exercício 8) Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
Ver solução completaQuestão 70
(Capítulo 14.8 – Exercício 36) Utilize os multiplicadores de Lagrange para dar uma solução alternativa aos exercícios da Seção 14.7 indicados.
Exercício 46
Ver solução completaQuestão 71
(Capítulo 14.8 – Exercício 39) Resolva pelo método dos multiplicadores de Lagrange o exercício da seção .
Determine as dimensões de uma caixa retangular de volume máximo tal que a soma dos comprimentos de suas arestas seja uma constante .
Ver solução completaQuestão 72
(Capítulo 14.8 – Exercício 4) Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
Ver solução completaQuestão 73
Os três números positivos suja soma é 12 e suja soma dos quadrados é a menor possível são:
Ver solução completaQuestão 74
(Capítulo 14.8 – Exercício 28) Use multiplicadores de Lagrange para demonstrar que o triângulo com área máxima, e que tem um perímetro constante p, é equilátero.
Ver solução completaQuestão 75
(Capítulo 14.8 – Exercício 9) Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
Ver solução completaQuestão 76
Seja e o domínio dado por . Então
- Ambos os valores de máximo e mínimo de em ocorrem no interior de .
- O valor máximo de em ocorre na fronteira de e o valor mínimo de em ocorre no interior de
- O valor mínimo de em ocorre na fronteira de e o valor máximo de em ocorre no interior de
- Ambos os valores máximo e mínimo de em ocorrem na fronteira de
- Nenhuma das demais alternativas
Questão 77
Use o Método dos Multiplicadores de Lagrange para encontrar os pontos da superfície que estão mais próximos da origem.
Ver solução completaQuestão 78
Sejam três números arbitrários tais que a soma vale . O menor valor possível para é :
- Não sei
Questão 81
Determine os pontos da superfície onde o plano tangente é paralelo ao plano .
Ver solução completaQuestão 82
Supondo que em alguma era passada ou futura a temperatura em cada ponto da superfície da Terra seja dada por . Considerando a Terra como uma esfera perfeita de raio , escolha a resposta completa:
- Como , não há como concluir o exercício
- A temperatura máxima ocorre em pontos distintos da Terra
- Existem infinitos pontos da Terra onde a temperatura é mínima, valendo graus
- A temperatura mínima ocorre em quatro pontos distintos da Terra
- A temperatura máxima é de graus.
Questão 83
A soma das coordenadas do ponto da superfície
Pertencente ao semiespaço superior e mais próximo da origem é:
Questão 84
Use o método dos multiplicadores de Lagrange para determinar os valores extremos de
Sobre a circunferência
Ver solução completaQuestão 85
(Capítulo 14.8 – Exercício 3) Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
Ver solução completaQuestão 86
Determine, se existirem, os pontos de máximo e mínimo absolutos de
No domínio
Ver solução completaQuestão 87
Determine os valores para de modo que o plano que passa pelo ponto forme, com os planos coordenados, o tetraedro no primeiro octante de vértices de volume mínimo.
Ver solução completaQuestão 89
Seja
- Encontre e classifique os pontos críticos de .
- Determine os pontos extremos globais de em
Questão 90
Encontre os extremantes da função objetivo no conjunto admissível (conjunto que satisfaz a restrição). Encontre também, se houve, os extremantes de em ℝ²
, sujeito à
Ver solução completaQuestão 91
Determine o volume máximo de uma caixa retangular inscrita numa esfera de raio .
Ver solução completaQuestão 93
1. (a) Utilize o método dos multiplicadores de Lagrange para encontrar as retas paralelas a reta e que sejam tangentes à elipse . Encontre os pontos de tangência.
Ver solução completaQuestão 94
Determine, caso existam, os valores de máximo e mínimo de sobre os seguinte conjunto:
Ver solução completaQuestão 95
Encontre os pontos da elipse mais próximos e mais distantes da origem.
Ver solução completaQuestão 96
4 - Determine o volume máximo de uma caixa retangular inscrita no elipsoide .
Ver solução completaQuestão 97
Determinar os valores da função sobre a esfera e classifique-os como máximo ou mínimo.
Ver solução completaQuestão 98
24. Encontre os extremantes da função objetivo no conjunto admissível (conjunto que satisfaz a restrição). Encontre também, se houver, os extremantes de em .
, sujeito à .
Ver solução completaQuestão 99
Quais os valores máximo e mínimo, respectivamente de
No domínio
- e
- e
- O valor máximo é e o valor mínimo não existe
Questão 101
Foi construída uma caixa com tampa, na forma de um paralelepípedo e com de volume. O material a ser utilizado nas laterais custa o dobro em relação ao que será utilizado na superfície do fundo. De acordo com sua resolução as dimensões da caixa que minimizam o custo do material são:
; ;
; ;
; ;
; ;
Ver solução completaQuestão 102
As dimensões da caixa retangular (com tampa) de volume máximo cuja área total de sua superfície é são:
Questão 103
Uma placa circular plana tem o formato da região . A placa (incluindo a fronteira ) é aquecida de modo que a temperatura em um ponto da placa é dada por . Determine as temperaturas no ponto mais quente e no ponto mais frio sobre a placa, incluindo a fronteira .
Ver solução completaQuestão 104
Considere a função
Definida na região dos pontos que satisfazem a relação
Então
- O valor mínimo absoluto de em é 0 e o valor máximo absoluto de em é 4. Há uma infinidade de pontos de mínimo e 4 pontos de máximo em .
- O valor mínimo absoluto de em é 0 e o valor máximo absoluto de em é 4. Há um ponto de mínimo e 4 pontos de máximo em .
- O valor mínimo absoluto de em é 0 e o valor máximo absoluto de em é 2. Há um ponto de mínimo e uma infinidade de pontos de máximo em .
- O valor mínimo absoluto de em é 0 e o valor máximo absoluto de em é 4. Há 4 pontos de mínimo e 4 pontos de máximo em .
- Nenhuma das demais alternativas
Questão 107
Denote por x, y, z três números positivos cuja soma é 100 e cujo produto é máximo. Assinale a alternativa correta:
- Os números são distintos dois a dois
- O produto máximo é
- Todas as demais alternativas estão erradas
Questão 108
Seja .
- Encontre e classifique os pontos críticos de .
- Encontre e classifique os pontos extremos globais de em .
Questão 109
Os valores máximos e mínimos absolutos da função restrita ao conjunto são, respectivamente:
e
Esta função não possui nem máximo, nem mínimo absolutos em
e
e
e
Ver solução completaQuestão 111
Seja e a circunferência . Qual das afirmativas abaixo é verdadeira?
- O máximo absoluto de em é e o mínimo absoluto de em é .
- Os valores extremos de em ocorrem em .
- O máximo absoluto de em é e o mínimo absoluto de em é .
- Os valores extremos de em ocorrem em e
- Não sei
Questão 112
Considere a função
Considere o conjunto
Calcule o valor máximo e o valor mínimo de restrita a .
Ver solução completaQuestão 113
Determine a equação do plano tangente à superfície , com e maiores do que , que forma um tetraedro mínimo com os planos coordenados.
Ver solução completaQuestão 114
Determine os pontos de máximo e mínimo da função
Sobre o conjunto compacto
Ver solução completaQuestão 115
Determine o volume do maior paralelepípedo no primeiro octante com três faces nos planos coordenados , e e um vértice no plano , onde .
Ver solução completaQuestão 116
Use multiplicadores de Lagrange e determine o máximo da função sobre o círculo
Ver solução completaQuestão 117
Determinar os pontos de máximos e mínimos e/ou mínimos da função dada, sujeita às restrições indicadas:
a)
com a condição de que
Ver solução completaQuestão 118
Determinar os pontos de máximos e mínimos e/ou mínimos da função dada, sujeita às restrições indicadas:
b)
com a condição de que
Ver solução completaQuestão 119
Determinar os pontos de máximos e mínimos e/ou mínimos da função dada, sujeita às restrições indicadas:
c)
; com a condição de que
Ver solução completaQuestão 120
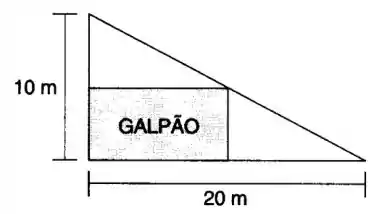
Um galpão retangular deve ser construído num terreno com a forma de um triângulo, conforme a figura a seguir. Determinar a área máxima possível para o galpão. Utilize o método dos multiplicadores de Lagrange.
Questão 121
Encontre a expressão geral (em termos de todos os parâmetros) do ponto que maximiza a função Cobb-Douglas sujeito a .
Ver solução completaQuestão 122
Seja
- Encontre e classifique os pontos críticos de
- Determine os extremos globais de em
Questão 123
Considere a função definida por
(a) Determine os pontos críticos de e classifique-os.
(b) Determine os pontos de máximo e mínimo absolutos de no conjunto
Ver solução completaQuestão 124
Seja e seja a curva
(a) Calcule os valores de máximo e mínimo global de restrita à curva .
(b) Determine em qual(is) ponto(s) de o valor máximo de é atingido e em qual(is) ponto(s) de o valor mínimo de é atingido.
Ver solução completaQuestão 125
Seja
Seja
Com .
Encontre os valores de máximos e mínimos globais de em .
Ver solução completaQuestão 126
(Capítulo 14.8 – Exercício 31) Utilize os multiplicadores de Lagrange para dar uma solução alternativa aos exercícios da Seção 14.7 indicados.
Exercício 41
Determine os pontos do que estão mais próximos do ponto (4,2,0).
Ver solução completaQuestão 127
Se é um ponto na esfera de raio
Que maximiza a função
Então o valor de é:
- Não exite nenhum ponto nas condições descritas acima.
