Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.6 - Ex. 24b

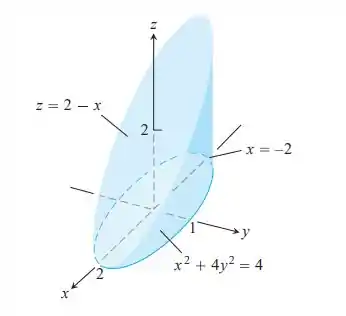
Um sólido de densidade constante é delimitado abaixo pelo plano z = 0 , dos lados pleos cilindro elíptico x 2 + 4 y 2 = 4   e acima pelo plano z = 2 - x   (veja a figura a seguir).

  1. Encontre x c . m   e y c . m
  2. Calcule a integral

M x y = ∫ - 2 2 ∫ - 1 2 4 - x 2 1 2 4 - x 2 ∫ 0 2 - x z   d z   d y   d x

Utilizando as tabelas integrais para realizar a integral final em relação a x. em seguida divida por M, para certificar-se de que z c . m = 5 4 .

Passo 1

Faaaala, cara! Tranquileba?

Achamos no item a) que M = 4 π

Passo 2

M x y = ∫ - 2 2 ∫ - 1 2 4 - x 2 1 2 4 - x 2 ∫ 0 2 - x z   d z   d y   d x

∫ - 2 2 ∫ - 1 2 4 - x 2 1 2 4 - x 2 1 2 z 2 0 2 - x d y   d x

∫ - 2 2 ∫ - 1 2 4 - x 2 1 2 4 - x 2 2 - x 2 2   d y   d x

∫ - 2 2 2 - x 2 2 y - 1 2 4 - x 2 1 2 4 - x 2 d x

∫ - 2 2 2 - x 2 2 4 - x 2     d x

Passo 3

∫ - 2 2 2 + x 2 2 - 2 x 4 - x 2     d x

E usando da propriedade de que a integral de uma soma é soma das integrais

2 ∫ - 2 2 4 - x 2 + 1 2 ∫ - 2 2 x 2 4 - x 2     d x   - 2 ∫ - 2 2 x 4 - x 2   d x

Para a primeira, temos uma função par e feitas as substituições teremos 4 π pela simetria da função; para a segunda temos uma função para um intervalo simétrico, logo feitas as substituições teremos 2 π , mas como é divido por 1 2 logo π ; e a terceira é uma função impar num intervalo simétrico, logo seu valor é 0. Sendo assim:

4 π + π + 0 = 5 π

Logo

M x y = 5 π

E sabendo que:

z c e n t = M x y M

Teremos

z c e n t = 5 π 4 π = 5 4  

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Encontre o centro de massa de uma solido de densidade constante delimitado inferiormente pelo paraboloide z = x 2 + y 2 e superiormente plano z=4Encontre o plano z = c que divide o solido em duas part
Mostre que o primeiro momento de inercia de um corpo no espaço em relação a qualquer plano passando pelo centro de massa do corpo é zero. (Sugestão, situe o centro de massa do corpo na origem e defina
O momento de inercia em relação a um diâmetro de uma esfera é sólida de densidade constante e raio a é 2 5 m a 2 , onde m é a massa da esfera. Encontre o momento de inercia e relação a uma reta tangen