Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.6 - Ex. 35a

  1. Mostre que o primeiro momento de inercia de um corpo no espaço em relação a qualquer plano passando pelo centro de massa do corpo é zero. (Sugestão, situe o centro de massa do corpo na origem e defina o plano como sendo y z . O que a formula x c e n t = M y z M então lhe diz?
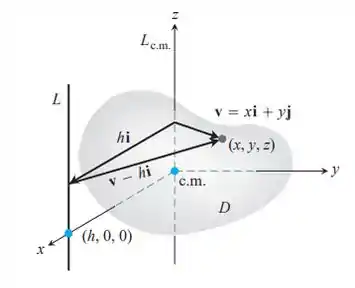
  2. Para provar o teorema dos eixos paralelos, situe o corpo com seu centro de massa na origem, coma reta L c . m ao longo do eixo z perpendicular ao plano x y no ponto h , 0,0 . Seja a região D do espaço ocupada pelo corpo. Então, na notação da figura:

I L = ∭ D v - h i 2   d m

Expanda o integrando e complete a prova.

Passo 1

Faaaala, cara! Tranquileba?

O primeiro momento de inercia é dado por M y z = x ( c . m )   M

Onde M é:

M = ∭ R δ   d x   d y   d z

Passo 2

Se temos que o plano passa pelo centro de massa, ou seja, em x c . m = 0

Passo 3

Isso nos implica dizer que:

M y z = ∭ R x δ x , y , z d x   d y   d z = 0

Logo

M y z = 0

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Momentos de inércia: encontre os momentos de inercia do sólido retangular mostrado aqui com relação as suas arestas calculando I x ,I y ,I z .
Momentos de inércia: os eixos coordenados na figura passam pelo centroide de uma cunha sólida paralelos às arestas identificadas. Encontre I x ,I y ,I z se a = b = 6 e c = 4 .
Um sólido de densidade constante é delimitado abaixo pelo plano z = 0 , dos lados pleos cilindro elíptico x 2 + 4 y 2 = 4 e acima pelo plano z = 2 - x (veja a figura a seguir).Encontre x c . m e y c .
Momento de inércia de uma esfera sólida Encontre o momento de inércia de uma esfera sólida de raio a em relação aodiâmetro. (Tome d = 1.)
Momento de inércia de um cone sólido Encontre o momento de inércia de um cone circular reto com raio de base ae altura h em relação ao seu eixo. (Sugestão: situe o cone comseu vértice na origem e seu