Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.7 - Ex. 2
Uma superfície é formada pelo cilindro , e por círculos no fundo e no topo. Suponha que você saiba que é uma função contínua com , e . Estime o valor de usando a soma de Riemann, tomando retalhos como os círculos do fundo e do topo, e a lateral dividida em quatro partes.
Passo 1
Fala, galera! =D
Precisamos estipular o valor de
Usando a soma de Riemann, para a superfície definida pelo cilindro
Com círculos no fundo e no topo, com
Os círculos na base e no topo pela equação tem raio igual a , já que
Logo, a área desses círculos será igual a:
Agora a área do corpo do cilindro será:
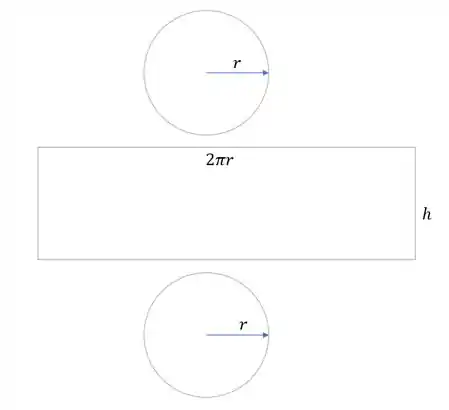
E por variar de até temos que a altura desse cilindro será igual a , nos dando uma área total de:
Logo cada de lado desse corpo será igual a:
Passo 2
Isso já nos dá capacidade de escrever a integral por soma de Riemann em:
Soma das bases + somas no corpo
Substituindo pelos valores dados no enunciado: