Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.7 - Ex. 11
Calcule a integral de superfície.
é a região triangular com vértices , e
Passo 1
E aí, minha gente! Beleza?
A questão quer o valor da integral:
é a região triangular com vértices , e .
Bom, para isso podemos usar a equação:
Então, vamos precisar achar as derivadas parciais da nossa função , que vamos achar usando os vértices que o enunciado apresentou. Daí, é só escrevermos nossa região como uma integral dupla e resolver nossa integral.
Bora lá!
Passo 2
Primeiro, vamos tentar achar nossa superfície descrita pelo enunciado:
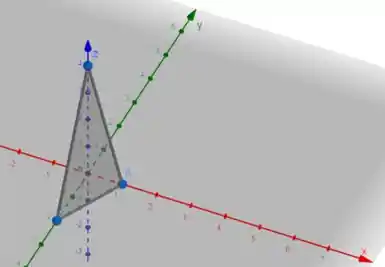
é a região triangular com vértices e
Galera, aqui vai ser a região do plano
Olhando no plano , vemos que:
E:
Então, agora que achamos nossa função , vamos calcular suas derivadas parciais
- Derivada em , tratando como constante:
- Derivada em , tratando como constante:
Calculando o termo da nossa equação:
Passo 3
Logo nossa integral se resume a
Tirando a constante para fora e integrando em , que é a integral de dentro, tratando como constante:
Aplicando os limites de integração em :
Agora integramos em :
Aplicando os limites:
Então: