Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.11 - Ex. 41 - b

Uma superfície S é representada pela equação vetorial r →   u , v   = 4 cos ⁡ u ,       4 s e n   u   ,       4 v

0 ≤ u ≤ 2 π

0 ≤ v ≤ 2

  1. Determinar a equação cartesiana de S
  2. Desenhar sobre a superfície S as curvas coordenadas obtidas fixando u = π 3 e v   =   1 , respectivamente
  3. Determinar o vetor ∂ r → ∂ u   x ∂ r → ∂ v   no ponto em que u = π 3 e v = 1 , representando -o no correspondente ponto P de S
  4. Supondo que uma lamina de densidade constante é representada por r →   u , v ,   determine o momento de inercia da lamina em relação ao eixo z

Passo 1

  1. Desenhar sobre a superfície S as curvas coordenadas obtidas fixando u = π 3 e v   =   1 , respectivamente

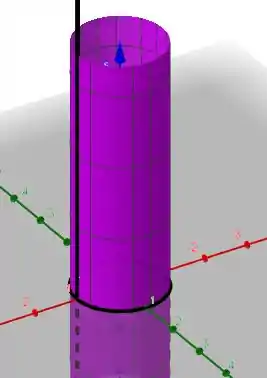
Quando fixamos um valor de um ângulo e deixamos a variável z livre temos apenas uma reta. A reta preta. Eu deixei exposta a superfície so pra termos uma ideia de que a reta parte ao espaço da nossa parametrização

Agora quando temos uma posição em z fixa e variamos o ângulo temos apenas um circulo na altura z fixada

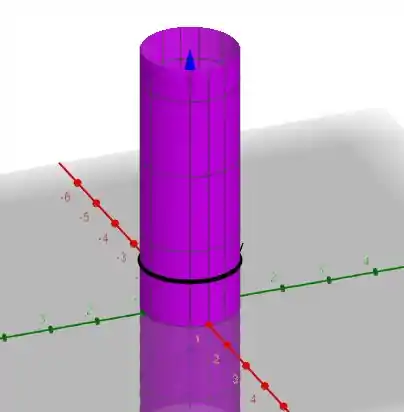
E esse é o resultado. Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de superfície. ∬ x 2 + y 2 d S , S é a superfície com equação vetorial. r u , v =2 u v , u 2 - v 2, u 2 + v 2, u 2 + v 2 ≤ 1
Calcule a integral de superfície. ∬ S xd S S é a região triangular com vértices ( 1,0 , 0 ) , ( 0 , - 2,0 ) e ( 0,0 , 4 )
Calcule a integral de superfície. ∬ S xd S S é a superfície z = 2 3 x 3 2 + y 3 2 , 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1
Encontre a área da superfície.Parte do paraboloide y = z 2 + x 2 que está no cilindro x 2 + z 2 = 16 .
Encontre a área da superfície.O helicoide (ou uma rampa espiral) com a equação vetorial r u , v = u cos ⁡ v i + u sen ⁡ v j + v k , 0 ≤ u ≤ 1 , 0 ≤ v ≤ π .