Enunciado
Cálculo Numérico - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.Revisão - Ex. 95
95. Suponha que num dado dia, numa certa cidade, a temperatura fahrenheit seja grus , t horas depois da meia – noite e . (a) Faça um esboço do gráfico de f. Ache a temperatura à (b) meia-noite;(c) 8 da manhã ;(d) meio dia ;(e) 2 da tarde e (f) 6 da tarde. (g) Ache a temperatura média entre 8 da manhã e 6 da tarde.
Passo 1
Para determinar o que ele quer no enunciado basta ir substituindo os valores de t na função dada no enunciado.
Passo 2
Letra (a)
O esboço do gráfico da função pode ser obtido utilizando o programa de computador Geogebra Online. Assim, o esboço do gráfico da função é:
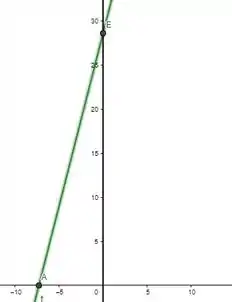
Passo 3
Letra (b)
A meia-noite t = 0h, sendo assim :
Passo 4
Letra (c)
As 8 da manhã t = 8h, sendo assim :
Passo 5
Letra (d)
Ao meio dia t = 12h, sendo assim :
Passo 6
Letra (e)
As duas da tarde t = 14h, sendo assim :
Passo 7
Letra (f)
As seis da tarde t = 18h, sendo assim :
Passo 8
Letra (g)
Daa definição 5.7.2 temos que se a função f for integrável no intervalo fechado [a,b], o valor médio de f em [a,b] será :
Assim, no nosso caso teremos que a temperatura média entre 8 da manhã e 6 da tarde será dada por :
Resposta
- Gráfico