Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.6 - Ex. 4
Suponha que uma força variável seja aplicada no sentido positivo do eixo , de tal forma que um objeto seja movido de até . Relacione o trabalho realizado pela força sobre o objeto com o valor médio de sobre e ilustre essa relação graficamente.
Passo 1
Queremos a relação entre o trabalho realizado por uma força variável e o valor médio dessa força.
A gente pode calcular a o trabalho realizado por uma força variável entre e , dessa forma:
Passo 2
Agora para calcular a força média, temos que lembrar como se calcula o valor médio de uma função:
Para a nossa força:
Passo 3
Agora vamos achar a relação entre essas duas coisinhas que a gente achou:
Vemos que a integral aparece nas duas expressões, então podemos escrever:
Ih olha só, descobrimos que a força média é igual o trabalho divido pela distância percorrida.
Passo 4
Para fazermos um gráfico dessa relação, podemos escrever:
O que é uma relação linear entre e a força média:
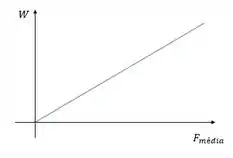
Resposta
