Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.2 - Ex. 44

Encontre o volume do sólido que resulta quando a região do Exercício 43 for girada em torno da reta y = - 1 .

Passo 1

Bom galera, nosso volume é dado pela rotação da região secção da função em torno de y = - 1 :

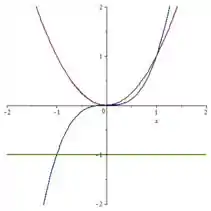
A gente pode chamar nosso raio externo de:

1 + x 2

O raio interno:

1 + x 3

E nossa região é:

0 ≤ x ≤ 1

Passo 2

Belezinha, a nossa integral para o volume é:

V = π ∫ 0 1 1 + x 2 2 - 1 + x 3 2   d x

= π ∫ 0 1 1 + 2 x 2 + x 4 - 1 + 2 x 3 + x 6   d x

= π ∫ 0 1 2 x 2 + x 4 - 2 x 3 - x 6   d x

Passo 3

Por fim, resolvemos a integral:

V = π ∫ 0 1 2 x 2 + x 4 - 2 x 3 - x 6   d x

= π 2 3 x 3 + x 5 5 - x 4 2 - x 7 7 0 1

= π 140 210 + 42 210 - 105 210 - 30 210 = 47 π 210

Resposta

47 π 210

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 0 ≤ x ≤ 8 e 0 ≤ y ≤ x 3
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 1 ≤ x ≤ e e 0 ≤ y ≤ l n x
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 0 ≤ x ≤ π e 0 ≤ y ≤ sin ⁡ x
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 0 ≤ x ≤ 1 e 0 ≤ y ≤ tan - 1 ⁡ x
(Volume de Sólido de revolução em torno do eixo y). Suponha f Estritamente crescente e com derivada contínua em [ a ,b ] , a ≥ 0ef a = 0 . Seja g : 0 , f b → a ,b A função inversa de f .Verifique que