Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 67
Um lote retangular deve ser cercado de forma que a área interna seja de . Sejam o comprimento da cerca necessária e o comprimento de um lado do retângulo; mostre que para e esboce o gráfico de versus para .
Passo 1
Então pessoal, como a área interna tem que ser , então temos que:
Então o perímetro da cerca é:
É claro, isso só é possível por ser um retângulo, ok? Show! Se isolarmos da expressão da área, teremos:
Substituindo na expressão de , teremos:
Que é exatamente o que queríamos demonstrar!
Passo 2
Para esboçarmos o gráfico de versus temos que determinar os pontos críticos da função , para podermos encontrar os extremos relativos e os pontos de inflexão (se existirem). Derivando teremos:
Igualando nossa derivada a zero:
A única forma disso dar zero é se:
Como , então podemos desprezar , ok? Ok, descobrimos que é um ponto crítico. Se adotarmos valores de menores que e depois maiores que notaremos que a derivada passa de negativa para positiva, o que indica um ponto de mínimo.
Passo 3
Por fim, vamos ver se a função apresenta pontos de inflexão:
Como , então não há valores para que seja nula. Dessa forma, teremos um gráfico parecido com:
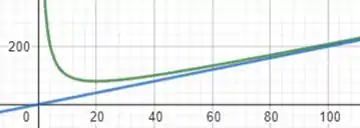
No qual a função em azul é a reta , que é nosso limite oblíquo! E está aí nossa resolução, pessoal!
Resposta
Ei, a resposta está no passo a passo :)