61. Considere a família de curvas .
a) Use um recurso gráfico computacional para gerar alguns membros dessa família.
b) Discuta o efeito da variação de na forma do gráfico e a localização tanto dos extremos relativos como dos pontos de inflexão.
Passo 1
a) Então galera, a função que nos foi dada é:
Encontrar alguns membros dessa família é dar alguns valores de para a nossa função. Vale ressaltar que .
Para :
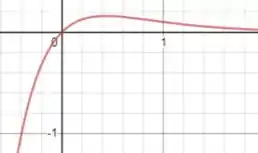
Para :
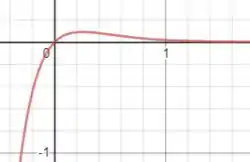
Para :
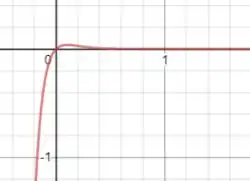
E esses são alguns membros da família de curvas que nos foi dada!
Passo 2
b) A primeira percepção que temos é de que quanto mais aumentamos o valor de , mais o gráfico “encolhe”, isso ocorre porque o expoente é negativo, então estamos aumentando o valor do denominador, o que resulta y menor, claro. Quanto aos extremos, temos que encontrar os pontos críticos da função que nos foi dada, então devemos encontrar a derivada de . Derivando nossa função, teremos:
Igualando nossa derivada a zero, teremos:
Como não pode ser zero, a única forma disso ser zero é se:
Que, pelo gráfico, sabemos que se trata de um ponto de máximo!
Passo 3
Agora vamos analisar os pontos de inflexão do gráfico! Encontrando nossa derivada segunda, teremos:
Igualando nossa derivada a zero, teremos:
Como não pode ser zero, então a única forma disso ser zero é se:
Note que assim como o ponto de extremo, o ponto de inflexão também possui no denominador! Se aumentarmos , o ponto de inflexão diminui, ou seja, é deslocado para a esquerda e se aproxima de , mas nunca chega a ser. É exatamente o que notamos nos gráficos do passo 1.
E está aí nossa resolução, pessoal!
Resposta
Ei, a resposta está no passo a passo :)