Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.Revisão - Ex. 78
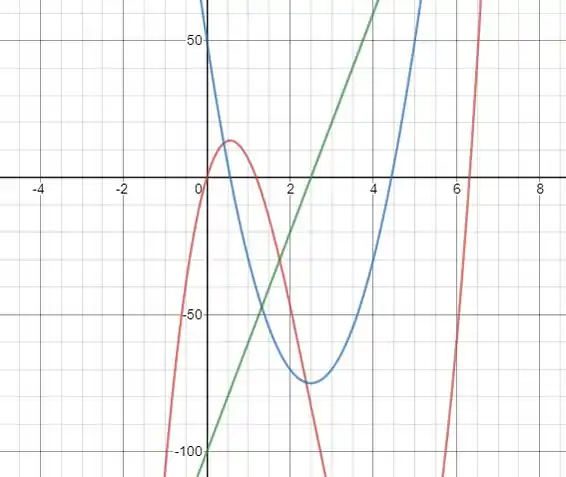
Suponha que a função velocidade de uma partícula movendo-se ao longo de um eixo seja m/s e que a partícula está na srcem no instante . Use um recurso gráfico computacional para gerar os gráficos de , e nos primeiros segundos do movimento.
Passo 1
Vamos achar as equações de e de , para encontrar vamos integrar a equação de :
Agora temos que achar a constante, vamos usar o dado do enunciado que na origem :
Assim temos:
Passo 2
Pronto, agora para achar a aceleração vamos derivar a velocidade:
Passo 3
Agora podemos traçar o gráfico das funções, com a de em vermelho, em azul e em verde:
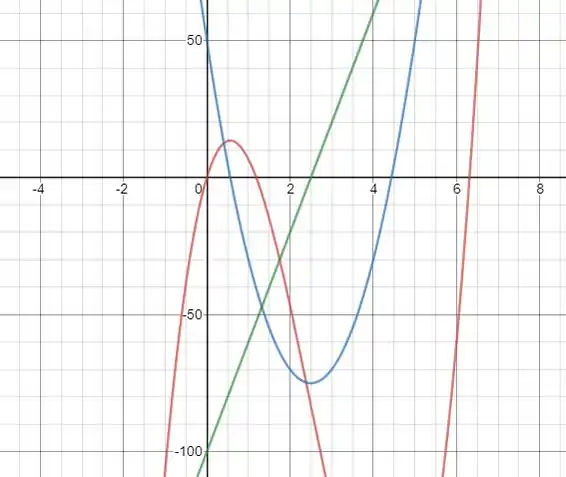
Resposta
Exercícios de Livros Relacionados
Em cada parte, use um CAS para resolver o problema de valor inicial. a d y d x = x 2 cos 3 x , y π 2 = - 1 b d y d x = x 3 4 + x 2 3 / 2 , y 0 = - 2
Faça uma crítica da “demosntração” seguinte de que toda constante de integração é nula. C = ∫ 0d x = ∫ 0 ⋅ 0d x = 0 ∫ 0d x = 0
Os campos de direções dados correspondem a uma das equações diferenciais abaixo. Identifique a equação diferencial que combina com a figura e esboce curvas e soluções pelos pontos destacados.
Os campos de direções dados correspondem a uma das equações diferenciais abaixo. Identifique a equação diferencial que combina com a figura e esboce curvas e soluções pelos pontos destacados.
Encontre uma equação da curva que satisfaz as condições dadas.Em cada ponto ( x ,y ) da curva, y satisfaz a condição d 2 y / d x 2 = 6 x ; a reta y = 5 - 3 x é tangente à curva no ponto onde x = 1 .