Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.2 - Ex. 63
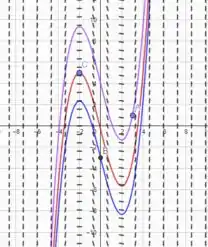
Os campos de direções dados correspondem a uma das equações diferenciais abaixo. Identifique a equação diferencial que combina com a figura e esboce curvas e soluções pelos pontos destacados.
Passo 1
Bom galera, aqui tem uma dica que eu vou dar pra matar essa questão, tá vendo que só em dois momentos a inclinação das direções parece ser , isso significa que a derivada da equação que a gente vai buscar tem duas raízes, logo a derivada é uma função quadrática, logo só pode ser:
Passo 2
Agora, vamos integrar isso:
Passo 3
Então precisamos achar as funções que passe pelos pontos , ) e . Usando o problema de valor inicial para descobrir o valor de , encontramos um para cada ponto e montamos as funções:
Plotando isso fica:
Resposta
Exercícios de Livros Relacionados
Use as desigualdades (12), (13) e (14) da Seção 7.7 para encontrar um número n de subintervalos para (a) a aproximação pelo ponto médio M n , (b) a aproximação trapezoidal T n e (c) a aproximação S n
Use as desigualdades (12), (13) e (14) da Seção 7.7 para encontrar cotas superiores para os erros nas partes (a), (b) e (c) dos exercícios indicados.Exercício 42.
Considere os seguintes métodos de calcular integrais: substituição u , integração por partes, frações parciais, fórmulas de redução e substituições trigonométricas. Em cada parte, dê a abordagem que v
Aproxime a integral usando (a) a aproximação pelo ponto médio M 10 , (b) a aproximação trapezoidal T 10 e (c) a aproximação S 20 pela regra de Simpson. Em cada caso, encontre o valor exato da integral
Aproxime a integral usando (a) a aproximação pelo ponto médio M 10 , (b) a aproximação trapezoidal T 10 e (c) a aproximação S 20 pela regra de Simpson. Em cada caso, encontre o valor exato da integral