Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.2 - Ex. 61
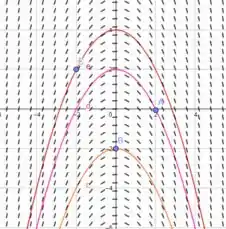
Os campos de direções dados correspondem a uma das equações diferenciais abaixo. Identifique a equação diferencial que combina com a figura e esboce curvas e soluções pelos pontos destacados.
Passo 1
Bom galera, se a gente observar a figura, notamos que ela parece poder formar uma parábola de equação do segundo grau com a concavidade para baixo, logo a derivada é para valores positivos é negativa, então a derivada que se encaixa nisso é:
Passo 2
Agora, vamos integrar isso:
Passo 3
Então precisamos achar as funções que passe pelos pontos , ) e . Usando o problema de valor inicial para descobrir o valor de , encontramos um para cada ponto e montamos as funções:
Plotando isso fica:
Resposta
Exercícios de Livros Relacionados
Calcule a integral usando a Tabela de Integrais. ∫ 1 x 4 x + 3d x
Calcule a integral usando a Tabela de Integrais. ∫ 3 x - 1 2 + x 2d x
Calcule a integral usando a Tabela de Integrais. ∫ tan 2 2 xd x
Calcule a integral usando a Tabela de Integrais. ∫ sin 7 x ⋅ cos 9 x d x
Calcule a integral usando a Tabela de Integrais. ∫ x 3 - x 2 e - x d x