Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.6 - Ex. 39

Suponha que as funções posição de duas partículas P 1 e P 2 , movendo-se ao longo de uma mesma reta, sejam

s 1 = 1 2 t 2 - t + 3 e s 2 = - 1 4 t 2 + t + 1

respectivamente, com t ≥ 0 .

  1. Prove que P 1 e P 2 não colidem.
  2. Qual é a menor distância entre P 1 e P 2 ?
  3. Durante quais intervalos de tempo elas se movem em sentidos opostos?

Passo 1

  1. Para provar que as partículas não colidem vamos subtrair as duas, e ver se possui alguma raiz, se tiver, temos que a diferença é zero, e elas colidem:

    2. s = s 1 - s 2 = 1 2 t 2 - t + 3 - - 1 4 t 2 + t + 1 = 1 2 t 2 - t + 3 + 1 4 t 2 - t - 1 =

    = 2 t 2 + t 2 4 - 2 t + 2 = 3 t 2 4 - 2 t + 2

    Igualando a zero:

    3 t 2 4 - 2 t + 2 = 0

    Temos que a expressão não possui raiz real, então elas não colidem.

    Passo 2

  2. Para achar a menor distância entre P 1 e P 2 vamos achar a expressão da velocidade e igualar a zero.

    3. Vamos então derivar a expressão:

    v t = s ' t = 3 t 2 4 - 2 t + 2 ' = 3 4 ⋅ 2 ⋅ t 2 - 1 - 2 + 0 = 3 2 t - 2

    Agora igualando a zero:

    3 2 t - 2 = 0 → 3 2 t = 2 → 3 t = 4 → t = 4 3

    Agora vamos analisar nesse ponto, e no ponto do intervalo t ≥ 0 para achar a menor distância:

    s 0 = 3 ⋅ 0 2 4 - 2 ⋅ 0 + 2 = 2

    s 4 3 = 3 ⋅ 4 3 2 4 - 2 ⋅ 4 3 + 2 = 3 ⋅ 16 9 4 - 8 3 + 2 = 16 3 4 - 8 3 + 2 = 16 3 ⋅ 1 4 - 8 3 + 2 = 4 3 - 8 3 + 2 =

    = 4 - 8 + 6 3 = 2 3

    Pronto, temos que a menor distância entre as partículas é de 2 3 .

    Passo 3

  3. Para saber quais intervalos de tempo elas se movem em sentidos opostos vamos analisar as velocidades separadas, vamos derivar:

v 1 ' = s 1 ' = 1 2 ⋅ 2 ⋅ t 2 - 1 - 1 + 0 = t - 1

v 2 ' = s 2 ' = - 1 4 ⋅ 2 ⋅ t 2 - 1 + 1 + 0 = - 1 2 t + 1

Vamos ver onde v 1 ' e v 2 ' são iguais a zero e analisar os sinais:

t - 1 = 0 → t = 1

- 1 2 t + 1 = 0 → t 2 = 1 → t = 2

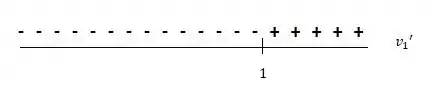
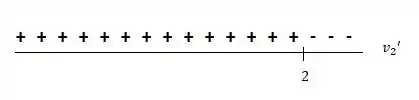
Assim, os intervalos de tempo que elas se movem em sentidos opostos são 0 ≤ t < 1 e t > 2 .

Resposta

  1. –
  2. 2 3
  3. 0 ≤ t < 1 e t > 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A função f cujo gráfico aparece abaixo tem valores dados na tabela a seguir.Use os dados da tabela para calcular os quocientes de diferenças f 3 - f 1 3 - 1 , f 2 - f 1 2 - 1 , f 2 - f 0 2 - 0 Usando
A função f cujo gráfico aparece abaixo tem valores dados na tabela a seguir.Use os dados da tabela para aproximar o valor das derivadas dadas. f ' 0,5 f ' 2,5
Encontre uma equação para a reta que é tangente à curva y = x 3 - 2 x + 1 no ponto 0,1 e use um recurso gráfico para fazer, na mesma tela, os gráficos da curva e de sua tangente.
O limite dado representa f ' a para alguma função f e algum número a . Encontre f x e a em cada caso. lim ∆ x → 0 ⁡ 1 + ∆ x - 1 ∆ x lim x 1 → 3 ⁡ x 1 2 - 9 x 1 - 3
Seja f x = 1 - x 2 . Use um argumento geométrico para encontrar f ' 2 2 .