Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 11.6 - Ex. 5

Suponha que as funções φ1, . . . , φn satisfazem a relação de ortogonalidade (1) e que uma função dada f(x) deve ser aproximada por Sn(x) = c1φ1(x) + . . . + cnφn(x), em que os coeficientes cn não são, necessariamente, os da Eq. (9). Mostre que o erro médio quadrático Rn dado pela Eq. (6) pode ser escrito na forma

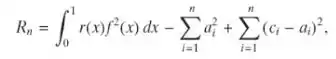
em que os ai são os coeficientes de Fourier dados pela Eq. (9). Mostre que Rn será minimizado se ci = ai para cada i.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos as deformações verticais de uma barra em suas condições de contorno. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser analisar a equação dada. Para a função, temos que:

R n = ∫ r ( x ) [ f ( x ) - S n x ] ² d x

R n = 2 ∑ c i ∫ r x f 2 x ϕ i x d x + ∑ ∑ c i   c j   ∫ r x f 2 x ϕ i x ϕ j x d x  

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

R n = ∫ r x f 2 x d x    

R n = ∑ a i ² + ∑ c i - a i 2

Resposta

R n = ∑ a i ² + ∑ c i - a i 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 14 a 20, encontre os autovalores e autofunções do problema de valores de contorno dado. Suponha que todos os autovalores são reais. y ' ' + λ y ' = 0 ; y ' 0 = 0 ; y L = 0
Em cada um dos problemas de 1 a 13, resolva o problema de valores de contorno dado ou mostre que não tem solução. y ' ' + 4 y = cos ⁡ x y ' 0 = 0;y ' π = 0
Em cada um dos problemas de 1 a 13, resolva o problema de valores de contorno dado ou mostre que não tem solução. y ' ' + 4 y = sen ⁡ x y 0 = 0;y π = 0
Em cada um dos problemas de 14 a 20, encontre os autovalores e autofunções do problema de valores de contorno dado. Suponha que todos os autovalores são reais. y ' ' + λ y = 0 ; y 0 = 0 ; y ' π = 0
Em cada um dos problemas de 14 a 20, encontre os autovalores e autofunções do problema de valores de contorno dado. Suponha que todos os autovalores são reais. y ' ' + λ y = 0 ; y ' 0 = 0 ;y π = 0