Suponha que em uma partícula esteja na origem de um eixo com uma velocidade . Nos primeiros segundos, não há aceleração e, então, uma força retardadora age produzindo uma aceleração negativa constante de .
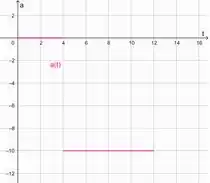
(a) Esboce a curva aceleração versus tempo no intervalo .
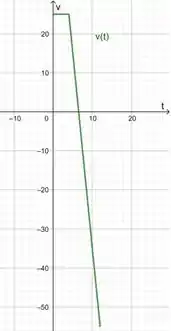
(b) Esboce a curva velocidade versus tempo no intervalo .
(c) Encontre a coordenada da partícula nos instantes e
(d) Qual é a coordenada máxima da partícula no intervalo ?
Passo 1
(a) Precisamos esboçar o gráfico da aceleração versus tempo, então vamos analisar como a aceleração variou como tempo.
Primeiro ele diz que não havia aceleração até o tempo . Então podemos escrever:
Depois ele diz que há uma aceleração constante igual a. Podemos dizer que:
Colocando isso em um gráfico:
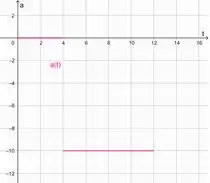
Passo 2
(b) Vamos esboçar o gráfico da velocidade versus o tempo, para isso, vamos ver como a velocidade variou.
O enunciado diz que a velocidade é constante em até , porque não há aceleração. Podemos dizer:
Mas depois entra a aceleração em cena. É aí que a gente lembra que:
Fazendo isso para o nosso valor de aceleração:
Podemos achar , porque sabemos que no tempo , a nossa velocidade ainda era e logo depois ela começa a diminuir. A gente pode escrever:
Como isso tudo está acontecendo entre e , podemos escrever:
Passo 3
Colocando esses dois intervalos no gráfico:
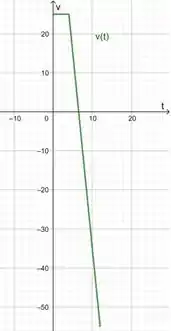
Passo 4
(c) Para encontrar a coordenada da partícula, podemos achar o deslocamento da partícula até o tempo desejado, que é dado pela fórmulinha:
Queremos o deslocamento entre e . Lembrando que:
Vamos precisar dividir nossa integral e escrever:
Passo 5
Vamos fazer o mesmo para o intervalo de até :
Passo 6
(d) A coordenada máxima acontece quando . A partir daí, a partícula começa a voltar a origem, porque a velocidade fica negativa.
Podemos descobrir em que instante isso acontece e depois calcular o deslocamento até esse instante.
Precisamos ver em que instante, no intervalo , a velocidade zera:
Agora calculamos o deslocamento de até :