Com referência à figura abaixo, encontre o valor e de forma que as áreas sombreadas sejam iguais.
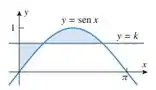
Passo 1
Para achar a área entre curvas, a gente monta a fórmula:
Vamos montar essa integral para essas duas áreas, e tentar chegar numa equação para achar . Vamos começar!
Passo 2
Para a primeira área, à esquerda, temos que a função é a maior e, é a menor. Um dos extremos de integração conseguimos ver pelo gráfico:
O segundo por enquanto vamos chamar de .
A integral fica:
Passo 3
Para a área à direita, a função maior é o seno e a menor é . Vamos chamar os extremos de integração de e , porque são valores mais complicados de achar agora. Vamos ter que mexer neles um pouco depois.
A integral fica:
Passo 4
Como as duas áreas devem ser iguais, podemos igualar as duas integrais e dizer que:
A gente pode fazer aparecer um sinal negativo na integral da direita, invertendo a ordem da subtração:
Aí a gente lembra da propriedade de integral:
Fazendo isso com as nossas integrais:
Passo 5
Chegou o momento de descobrirmos quem é , para abrirmos essa integral. Temos que é a interseção de e :
Substituindo isso na nossa integral:
Calculando a integral:
Passo 6
Agora a gente usa um CAS para resolver essa equação. Vamos usar o do Geogebra, que dá para acessar pelo navegador.
Se jogar essa equação direto na calculadora CAS (trocando a variável pela variável do gráfico do programa, ), ela vai te dar um gráfico cheio de retas paralelas. Isso acontece porque essa equação tem várias soluções.
Mas repara na nossa figura que precisa ser um valor no intervalo . Logo, só há uma solução que serve para gente:
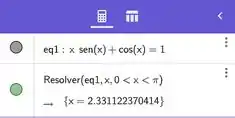
Logo:
Mas a gente quer o . É só lembrar que: