Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 52
Suponha que a refinaria do Exercício 51 esteja localizada ao norte do rio. Onde deveria estar situado?
Passo 1
Fala aí! como vai?
Nesse problema temos que repetir o problema 51 mas com novas variáveis...
Nesse caso, uma refinaria está a a norte da margem de um rio com de largura e nosso objetivo é ligar um oleoduto até um ponto a a leste do rio. Sendo que o custo para construir o oleoduto sobre a terra é de e sob o rio.
A partir daí queremos saber onde um ponto deve ser localizado na margem do rio para que o custo de construção seja o menor possivel.
Tem ideia de como fazemos isso?
Para resolver esse problema, vamos desenvolver uma equação que descreve o custo em função do ponto à margem do rio e a partir daí aplicar a metodologia dos pontos críticos de uma função para minimizar o custo.
Sacou? Bora começar!
Passo 2
Vamos começar desenhando nosso problema...
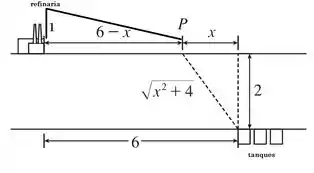
A nova distância de até a refinaria é:
Portanto, a nova função custo é:
Onde é a distância da refinaria até o ponto e a distância do ponto até os tanques.
Pela imagem, temos
Tranquilo até aqui?
Passo 3
Agora minimizamos a função derivando e igualando a .
Pela regra da cadeia temos que
Igualando essa função a , temos
Simplificando os dois lados por ...
Para simplificar essas raízes vamos elevar os dois lados ao quadrado
Vamos passa tudo para um lado...
Com o auxílio de uma calculadora vamos encontrar as raízes desse polinômio...
Nesse caso, não faz sentido pois é negativo, então vamos considerar apenas .
Show?
Passo 4
Agora vamos analisar o custo em e comparar com os custos dos extremos do nosso domínio... e .
Para
Agora para
E para
Comparando os três resultados, vemos que em o custo é menor. Logo, o ponto deve estar localizado a
A leste da refinaria.
E aí! entendeu tudo? Responde Aí!
Resposta
deveria estar a aproximadamente a leste da refinaria.