Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.3 - Ex. 86
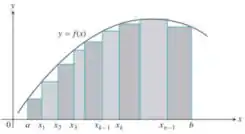
86. Suponha que seja contínua e não negativa em , como na figura a seguir. Ao inserir pontos
como mostrado, divida em subintervalos de comprimentos , que não precisam ser iguais.
a) Se , explique a relação entre a soma inferior:
e as regiões sombreadas na primeira parte da figura.
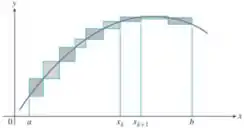
b) Se , explique a relação entre a soma superior:
e as regiões sombreadas na segunda parte da figura.
c) Explique a relação e as regiões sombreadas ao longo da curva na terceira parte da figura.
Passo 1
a) A conclusão que chegamos observando a figura é bastante tranquila galera, mesmo que não pareça tanto. Dando um spoiler, a resposta da b) também é bem de boa, beleza? Sabendo que a área dos retângulos é igual ao produto da lagura pela altura, então temos o seguinte:
Essa resposta faz sentido porque a região sombreada é a soma da área de todos os retângulos que estão inscritos. Ademais, vale evidenciar também que essa somatória acima são as áreas de que estamos falando, tudo bem?
Passo 2
b) A conclusão é LITERALMENTE a mesma que a da letra a), mas com uma diferença, de que não estamos mais falando de mínimos e sim de máximos. Sendo assim:
E, assim como fizemos na letra a), vale evidenciar também que essa somatória acima são as áreas de que estamos falando, de boas?
Passo 3
c) Então galera, se prestarmos atenção na terceira figura, é facilmente notável que aquela regiãozinha rachurada é a diferença entre a região da segunda figura e a da primeira figura . A relação é esta.
Resposta
Ei, a resposta está no passo a passo :)