Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 5
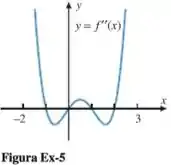
Use o gráfico da equação na figura Ex-5 para determinar as coordenadas de todos os pontos de inflexão de . Explique seu raciocínio.
Passo 1
Aqui o objetivo é tentar determinar as coordenadas dos pontos de inflexão, ou seja, dos pontos em que vemos a mudança de concavidade da função.
Pela visualização do gráfico é fácil perceber esses pontos, pelo comportamento da função.
Tomando como referência os pontos -2 e 3, já dados no gráfico, é possível perceber que entre -1 e 0, mais ou menos em temos o primeiro ponto de inflexão.
Passo 2
O segundo ponto ocorre mais ou menos em , quando o gráfico passa da concavidade pra cima à concavidade pra baixo novamente.
O terceiro ponto ocorre em , quando novamente a concavidade inverte, agora sendo pra baixo à pra cima.
A partir desse ponto, a função se mantém com a concavidade voltada pra cima até o infinito.
Resposta
Pontos:
;
;