Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.2 - Ex. 46

Suponha que a e b sejam vetores não nulos, não paralelos e que c seja um vetor pertencente ao plano determinado por a   e b . Dê um argumento geométrico para mostrar que c pode ser escrito como c = s a + t b para uma escolha conveniente de s e t . Depois dê argumentos usando componentes.

Passo 1

Fazendo o desenho da situação descrita, ficamos com:

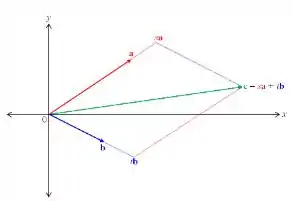
Agora para argumentar com as componentes vamos dizer que nossos vetores são a = a 1 , a 2 ,   b = b 1 , b 2   e   c = c 1 , c 2 . Então c = s a + t b   significa que

c 1 , c 2 = s a 1 , a 2 + t b 1 , b 2

= s a 1 , s a 2 + t b 1 , t b 2 = ( s a 1 + t b 1 , s a 2 + t b 2 )

Então c 1 = s a 1 + t b 1 e c 2 = s a 2 + t b 2 .

O argumento aqui é que essas duas equações formam um sistema de equações lineares que tem uma solução única para os valores de s e t , já que a e b não são paralelos (não são múltiplos um do outro)

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dados os vetores u → = ( 2 , - 3 , - 1 ) e v → = ( 1 , - 1,4 ) d) u → + v → * ( v → - u → )
Dados os vetores u → = ( 2 , - 3 , - 1 ) e v → = ( 1 , - 1,4 ) , calcular: 2 u → * ( - v → )
Sejam os vetores u → = 2 , a , - 1 ,v → = ( 3,1 , - 2 ) e w → = ( 2 a - 1 , - 2,4 ) . Determinar a de modo que u → ∙ v → = u → + v → ∙ v → + w →
Dados os pontos A 4,0 , - 1 , B ( 2 , - 2,1 ) e C ( 1,3 , 2 ) e os vetores u → = 2,1 , 1 e v → = ( - 1 , - 2,3 ) , obter o vetor x → tal que: 3 x → + 2 v → = x → + A B → ∙ u → v →
Dados os vetores u → = ( 2 , - 3 , - 1 ) e v → = ( 1 , - 1,4 ) b) u → + 3 v → * ( v → - 2 u → )