Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 1.2 - Ex. 8
Suponha um tanque na forma de um cilindro circular reto de raio e altura . O tanque está inicialmente cheio de água, e a água vaza por um orifício circular de raio no fundo. Use as informações do Problema 7 para obter a equação diferencial para a altura da água em qualquer instante de tempo .
Passo 1
Vamos lá, a primeira coisa que a gente tem que fazer para entender o exercício, é visualizar o que ta acontecendo ali. Mas pode relaxar que eu já trouxe o desenhinho pra gente sacar qual é a desse problema.
O tal do tanque na forma de um cilindro circular reto é assim olha:
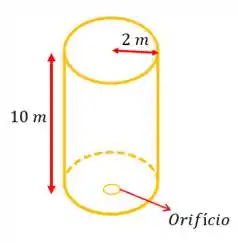
E o que acontece aqui é que esse tanque ta cheio de água, mas essa água ta vazando por aquele orifício ali embaixo, sacou?
Então agora pensando no tanque com água:
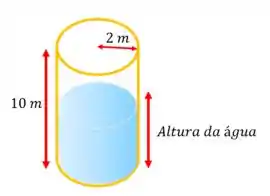
Concorda comigo que conforme a água vaza pelo orifício, a altura da água vai diminuindo? É exatamente essa variação da altura da água que vai ser a base da nossa equação diferencial :P Então queremos encontrar uma equação diferencial que nos dê , bora lá!
Passo 2
O enunciado nos disse pra utilizar as informações do problema 7, e lá ele fala pra gente que, considerando o atrito, o volume de água que sai do tanque por segundo é aproximadamente , ou seja:
Onde o sinal de menos quer dizer que o volume ta diminuindo, é a área do orifício, é a aceleração da gravidade e é a altura do tanque.
Mas isso aí é , como podemos fazer pra chegar no ?
Passo 3
Vamos pensar no volume que a água ocupa dentro do tanque, ele pode ser dado por:
Como é a área da superfície da água, ou seja, a parte que não depende da sua altura, vamos chamar de uma variável
Derivando os dois lados em relação a :
Ta bom, mas acabamos de ver que não depende da altura e também não depende de , então ele vai ser uma constante, podendo sair pra fora da derivada:
Boaaa, encontramos outra expressão pra que envolve o que queremos: !!
Agora é só substituir isso lá na expressão .
Passo 4
Pelos dados do exercício 7, temos:
E pelas manipulações que fizemos no passo 3, temos:
Substituindo em :
Ihuuuuu, encontramos a expressão para , arrasamos né??
Agora é só substituir os valores dados pelo exercício!!
Passo 5
Beleza, encontramos que a expressão para a altura da água em função do tempo é
Agora vamos substituir os valores.
Temos que é a área do orifício. Como o orifício é circular, sua área vai ser dada por , onde é o seu raio em , então antes vamos fazer a conversão:
Assim,
E por fim, o é a área da superfície da água, que vai ser dada por , sendo que é o próprio raio do tanque, certo? Então,
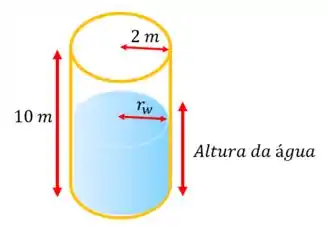
Portanto:
Passo 6
Substituindo os dados do passo 5 na expressão de :
De acordo com o exercício 7, temos
Ufaa, encontramos!!