Suponha que um tubo oco gire com uma velocidade angular constante de ω rad/s em torno de um eixo horizontal em um extremo do tubo, conforme a figura a seguir. Suponha que um
objeto deslize sem atrito dentro do tubo, enquanto o tubo estiver girando. Seja r a distância do objeto ao ponto pivô no instante e suponha que, quando , o objeto esteja em
repouso e . Pode-se mostrar que, se o tubo estiver na horizontal em e girando conforme a figura, então
durante o período em que o objeto estiver no tubo. Suponha
que esteja em segundos, esteja em metros, e .
(a) Faça o gráfico de r versus t para .
(b) Supondo que o tubo tenha um comprimento de 1 m, aproximadamente quanto tempo o objeto levará para atingir o final do tubo?
(c) Use o resultado de (b) para aproximar , no momento em que o objeto atingir o fim do tubo.
Passo 1
Bom galera, usando um recurso computacional, temos que esse gráfico será:
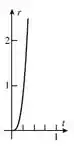
Para encontrarmos o item (b) que é o tempo que o objeto levará para atingir o final do tubo, temos:
Passo 2
Agora, para o item (c), começamos derivando a expressão:
Prontinho!!
Resposta
(a) 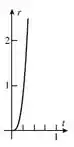
(b)
(c)