Suponha que você tenha acabado de servir uma xícara de café recém-coado com uma temperatura de em uma sala onde a temperatura é de .
- Quando você acha que o café esfria mais rapidamente? O que acontece com a taxa de resfriamento com o passar do tempo? Explique.
- A Lei de Resfriamento de Newton afirma que a taxa de resfriamento de um objeto é proporcional à diferença de temperatura entre o objeto e sua vizinhança, desde que essa diferença não seja muito grande. Escreva uma equação diferencial para expressar a Lei de Resfriamento de Newton nessa situação particular. Qual a condição inicial? Tendo em vista sua resposta na parte (a), você acha que essa equação diferencial é um modelo apropriado para o resfriamento?
- Faça um esboço para o gráfico da solução do problema de valor inicial na parte (b).
Passo 1
- Nessa questão podemos usar nossos conhecimentos do dia-a-dia e pensar que quanto maior a diferença entre as temperaturas, mais rápido o café irá resfriar. Quanto mais o tempo passa mais essa diferença diminui, então a velocidade de resfriamento diminui conforme o tempo passa.
- Pela Lei de Resfriamento de Newton, a taxa de resfriamento de um objeto é inversamente proporcional à diferença de temperatura entre ele e o ambiente. Precisamos encontrar uma equação diferencial que satisfaça isso e ver se condiz com nossa explicação do item (a).
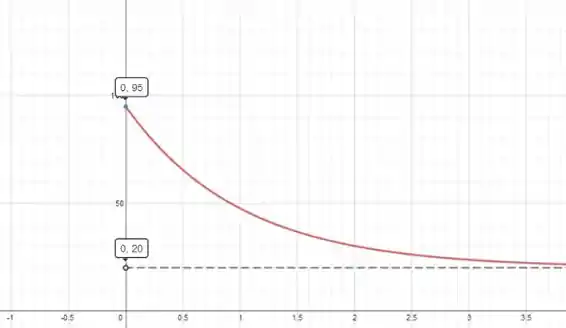
- Precisamos esboçar um gráfico onde e .
Passo 2
Passo 3
Vamos chamar a temperatura do café de , então a taxa de variação da temperatura ao longo do tempo é . A constante de proporcionalidade será chamada de sendo , e a diferença é igual a . Então:
Note que existe um valor negativo na equação para indicar que ela decresce quando . Assim, .
Essa equação respeita o que dissemos no item (a), pois quanto menor a diferença de temperatura, menor a taxa de resfriamento.
Passo 4
Também sabemos que a temperatura sempre decresce, até se igualar com a temperatura ambiente de , então podemos desenhar o gráfico:
Resposta
Ei, a resposta está no passo a passo :)