Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 7.4 - Ex. 23
- Suponha que você tenha três algoritmos diferentes para resolver o mesmo problema e que cada um deles dependa de uma série de passos que é da ordem de uma das funções listadas aqui:
Qual dos algoritmos é mais eficiente a longo prazo?
- Trace em um mesmo gráfico as funções do item a para obter uma noção da velocidade com que cada uma cresce.
Qual dos algoritmos é mais eficiente a longo prazo?
Passo 1
Galera, queremos saber quais dos algoritmos é mais eficiente. Portanto, estamos diante de uma questão sobre taxas relativas de crescimento. Vamos calcular os limites??
Assim, cresce mais lentamente que . Agora, vamos verificar para a função que ainda falta.
cresce mais lentamente que .
Assim, concluímos que o algoritmo mais eficiente é
Passo 2
A imagem gráfica será:
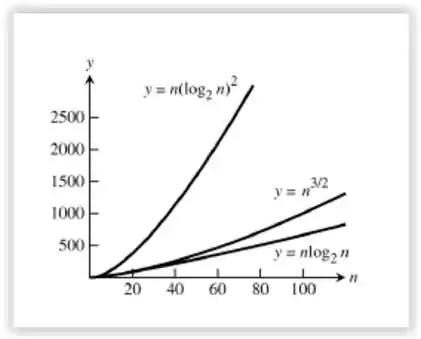
Resposta
- o algoritmo mais eficiente é
- Gráfico
Exercícios de Livros Relacionados
(a) Explique por que a regra de L’Hôpital não se aplica ao problema lim x → 0 x 2 sin 1 x sin x (b) Encontre o limite
O modelo de crescimento logístico dado na Fórmula (1) é equivalente a: y e k t + A y = L e k t Em que y é a população no instante t t ≥ 0 e A , k e L são constantes positivas. Use a derivação implícit
Suponha que a disseminação de um vírus de gripe em um campus universitário seja modelado pela função: y t = 1000 1 + 999 e - 0,9 t Onde y t é o número de estudantes infectados no instante t (dado em d
Seja f x = x 2 sin 1 x .(a)Os limites lim x → 0 + f ( x ) e lim x → 0 - f ( x ) são formas indeterminadas?(b)Use um recurso computacional para gerar o gráfico de f e use o gráfico para fazer con
Se x 1x 2 , que relação deve existir entre f ( x 1 ) e f ( x 2 ) para f ser crescente em um intervalo contendo x 1 e x 2 ? Decrescente? Constante ?Qual condição f ' garante que f seja crescente em um