Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 69
Suponha que a disseminação de um vírus de gripe em um campus universitário seja modelado pela função:
Onde é o número de estudantes infectados no instante (dado em dias, começando em ). Use um recurso gráfico para estimar o dia em que o vírus está sendo disseminado mais rapidamente.
Passo 1
Então galera, o que temos que fazer aqui é encontrar um valor de no qual é máximo, jóia? Como o enunciado não quer que calculemos nada, vamos apenas plotar o gráfico dessa função e tentar estimar esse valor de que tanto queremos! Plotando, teremos:
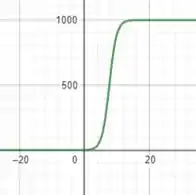
E do gráfico tiramos que o dia em que o vírus está sendo disseminado mais rapidamente é em .
Resposta
Exercícios de Livros Relacionados
Determine os intervalos de crescimento e de decrescimento e esboce o gráfico (calcule para isto todos os limites necessários). f x = x 3 - x 2 + 1 x
Determine os intervalos de crescimento e de decrescimento e esboce o gráfico (calcule para isto todos os limites necessários). y = x 2 + 1 x
Determine os intervalos de crescimento e de decrescimento e esboce o gráfico (calcule para isto todos os limites necessários). x = t 1 + t 2
Calcule. lim x → 0 ⁻ x e 1 x ⁻
Seja f x = e - 1 x 2 s e x ≠ 0 0 s e x = 0 Calcule f ' 0 , pela definiçãoDetermine f ' Esboce o gráfico, calculando, para isto, todos os limites necessários