Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 67

Seja .

(a)Os limites e são formas indeterminadas?

(b)Use um recurso computacional para gerar o gráfico de e use o gráfico para fazer conjecturas sobre os limites em (a).

Passo 1

(a)Se aplicássemos diretamente em , dentro da função, obviamente teríamos uma forma indeterminada, pois teríamos o seno de um ângulo , que é indeterminado.

Mas esses limites são calculáveis pelo Teorema do Confronto, em que a gente faz o seguinte procedimento:

Passo 2

Primeiro, lembramos da trigonometria básica que o seno de um ângulo (que, nesse caso, é descrito por ) está limitado entre e . Escrevemos então:

Agora, repara que se a gente multiplicar cada termo da inequação por a gente vai ter:

Que, no termo do meio, resulta exatamente na nossa função . O Teorema do Confronto diz que, quando uma função é limitada entre outras duas, o limite dessas funções dos extremos a um determinado valor, também vai valer pra função do meio!

Como assim? Vamos ver melhor:

Passo 3

Se queremos e , basta a gente calcular esses mesmos limites pras funções que limitam , que são e .

Então fazemos:

Tendo todos esses limites valendo , então, pelo Teorema do Confronto, nos resta a conclusão de que:

Passo 4

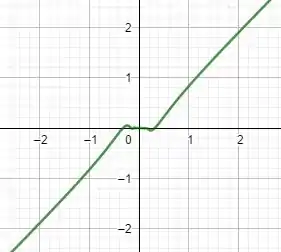
Pelo gráfico da função, fica claro que, se aproximando de 0 pela esquerda ou pela direita a função se aproxima de 0. Comprovamos assim que os limites de fato não são indeterminados!