Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.2 - Ex. 23 b
A tabela dá as alturas vencedoras do salto com vara nas olímpiadas de até 2004:
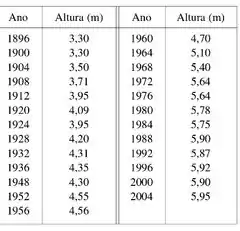
- Encontre e faça um gráfico da reta de regressão.
Passo 1
Eaeee, belezinha!!! Bom... a questão nos dá uma tabela contendo as alturas vencedoras do salto com vara nas olímpiadas de até 2004:
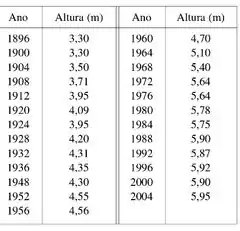
Com essa tabela a questão quer que a gente faça um gráfico da reta de regressão. Você lembra da equação?
Mas como essa questão é uma continuação, já vimos isso antes!
Na verdade, a gente acabou fazendo isso na letra a) quando ela nos perguntou se um modelo linear é apropriado. E ele é!
Então a ideia aqui é com a ajuda de um programa, achar os coeficientes dessa reta!
Então vamos relembrar!! 😉
Passo 2
Bom... Primeiramente, do gráfico de dispersão para os valores dados na tabela a gente tem:
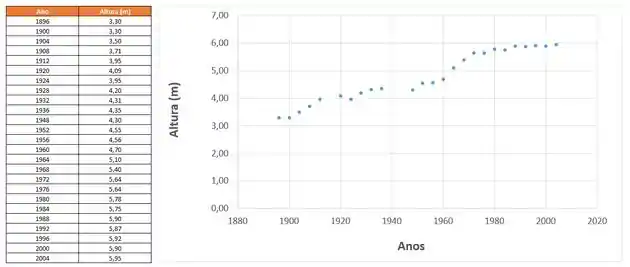
Obs: utilizamos o Excel porque é necessária uma ferramenta gráfica para a gente ver melhor 😉.
Tudo bem até aqui?
Passo 3
Ainda, com a ajuda do Excel vamos tentar aproximar os pontos, através de uma “regressão linear”.
Em outras palavras, vamos aproximar os pontos por uma reta. A ideia é selecionar esses pontos dessas colunas e clicar na função regressão linear! Ele vai nos fornecer uma equação e uma reta: a que melhor se adapta aos pontos! Nem sempre a reta vai passar por eles, mas na média é a que fica mais próxima de todos eles!
Ao fazer isso, temos:
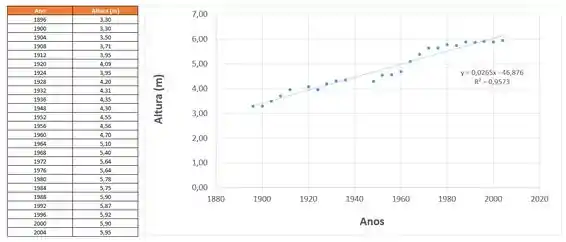
Perceba que os pontos se aproximam bem da reta de equação:
Em que é a altura e é o ano.
Entendeu direitinho?? Responde aee!! 😉