Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.6 - Ex. 45
45. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas.
Passo 1
Opa, vamos fazer essa questão! Temos a seguinte curva:
E o enunciado pede pra a gente encontrar as suas as assíntotas horizontais e verticais e depois confirmar que o cálculo está certo esboçando o gráfico da função!
Para acharmos as assíntotas horizontais, vamos analisar o limite da função quando tende para e . Sendo a assíntota:
Ou
Já as assíntotas verticais geralmente estão relacionadas a um valor de onde a o valor da nossa função não vai para ou .
Ou
Bora colocar a mão na massa então!
Passo 2
Começando pelas assíntotas horizontais, vamos analisar os limites para tendendo a e .
Assim, para tendendo a :
Concorda comigo que quando então:
Então vamos reescrever o nosso limite assim:
Sempre poderemos fazer isso quando tivermos na função um quociente entre duas funções polinomiais.
Então:
Agora para tendendo a , temos que:
Como não chegamos a uma constante no cálculo dos limites, isso nos diz que não temos nenhuma assíntota horizontal!
Passo 3
Agora vamos analisar as assíntotas verticais, isto é, quando nossa curva vai pro infinito. Lá em cima falamos que assíntotas verticais estão relacionados a um ponto onde a nossa função não está definida, vamos observar a nossa função:
Podemos tentar dar uma simplificada nela fatorando o numerador e o denominador.
Então, simplificando o , ficamos com:
O quando o denominador é zero, isto é:
Portanto teremos uma assíntota vertical em:
Passo 4
Fazendo um gráfico, temos:
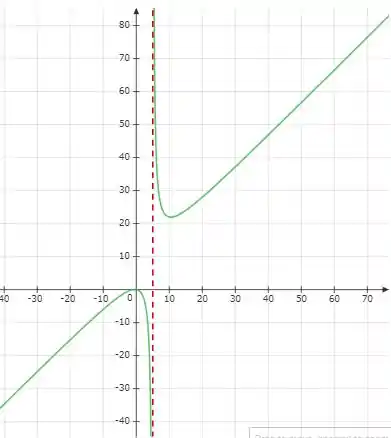
Pelo gráfico, podemos confirmar que as assíntotas é realmente em .
Resposta
Assíntota vertical: