Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.8 - Ex. 37
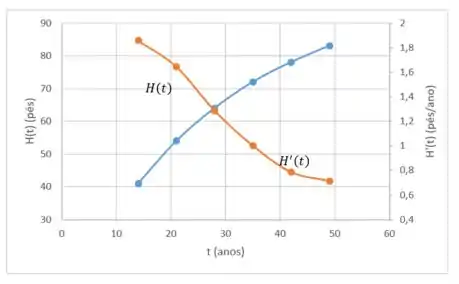
A tabela indica a altura com o passar do tempo de um pinheiro típico árvore cultivada para madeira serrada em um site gerenciado.
Se for a altura da árvore após anos, construa uma tabela dos valores estimados para e esboce seu gráfico.
Passo 1
E aí, bora resolver esse problema?! O enunciado nos dá a seguinte tabela:
Aqui temos a altura de uma árvore ao longo dos anos. O que temos que fazer aqui é construir uma tabela estimada pra , considerando que descreve a altura da árvore em função da sua idade.
Beleza, então será a variação da altura de acordo com os anos e pra fazer a estimativa vamos fazer o seguinte cálculo:
Vamos pegar sempre dois pontos consecutivos, como por exemplo:
Pra calcular os pontos que não estão na extremidade vamos tirar uma média entre a aproximação por dois lados, vou mostrar com o :
Então será a média entre e . Sacou?!
Com a tabela em mãos vamos esboçar o gráfico de . Essa parte é muito simples, o eixo é o e o eixo o tempo . Só precisamos jogar os dados no gráfico e ligar os pontos!
Passo 2
Vamos começar pelos pontos das extremidades que são mais simples:
Agora :
No numerador a unidade é e no denominador , então a unidade de é .
Passo 3
Agora vamos para os pontos do meio:
Agora pegamos e :
A média dos dois é:
A continha é bem simples e vai se repetindo, fazendo o mesmo com todos os outros anos a gente encontra:
Passo 4
Show de bola, a gente pega pontos de e para formar gráficos:
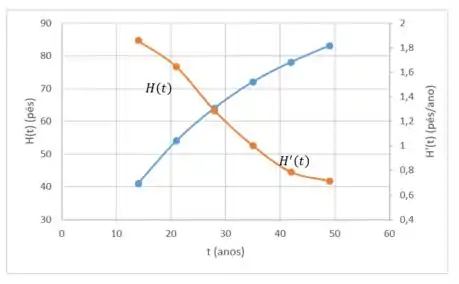
Repara que nos primeiros anos tem uma inclinação maior, portanto a sua derivada é maior e com o passar dos anos a inclinação só vai diminuindo e com isso diminui!
Resposta
