Quando você abre uma torneira de água quente, a temperatura da água depende de quanto tempo a água está fluindo.
(a) Esboce um gráfico possível de em função do tempo que decorreu desde que a torneira foi aberta.
(b) Descreva como é a taxa de variação de em relação a quando está crescendo.
(c) Esboce um gráfico da derivada de .
Passo 1
Faaala, gente bonitaa! Tudo certinho com vocês?
Essa questão pede pra imaginarmos uma torneira de água quente e pergunta como a temperatura da água evolui com o tempo.
O enunciado divide essa pergunta em três partes:
No item (a), precisamos esboçar o gráfico de em função do tempo desde que a torneira é aberta.
O item (b) pede pra descrevermos como se comporta a taxa de variação de ao longo do tempo .
E pra fechar, o item (c) pede pra esboçarmos o gráfico da derivada de .
A primeira coisa que percebemos é que ele não um pingo de informação pra gente, né? Ele espera que a gente saiba como funciona o aquecimento da torneira??
Pior que é isso mesmo... Mas não surta ainda! Vamos tentar passar por esse processo de maneira resumida. Olha só:
Tenta imaginar que o aquecimento da água acontece em três partes diferentes:
Primeiro nós temos o fluxo daquela água em temperatura ambiente que já estava prestes a sair da torneira. Não dá tempo de aquecer essa porção da água antes dela sair.
Depois a água começa a ser aquecida e a sua temperatura começa a aumentar.
Só que essa temperatura não aumenta indefinidamente, certo? O que acontece, por fim, é que a água alcança uma determinada temperatura de uso e se mantem constante!
Agora que temos uma noção melhor de como as coisas funcionam, vamos pensar juntos sobre essa questão.
Passo 2
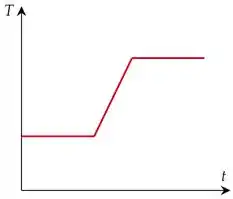
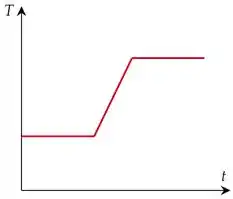
Vamos tentar atacar o item (a). Precisamos fazer um esboço do gráfico de .
Relembrando e resumindo, as três partes do aquecimento da água são:
Parte 1: Água em temperatura ambiente que já estava prestes a sair da torneira. Temos temperatura constante nesse intervalo.
Parte 2: Água aquecendo até atingir temperatura de uso. Temperatura subindo.
Parte 3: Água em temperatura de uso. Temperatura constante.
O gráfico fica mais ou menos assim:
Boa! Vamos pro próximo item.
Passo 3
O item (b) pede pra descrevermos como se comporta a taxa de varia�o de .
De certa maneira, nós já fizemos isso pra entender como esboçar o gráfico, mas vamos oficializar.
Primeiramente, a temperatura é constante, o que significa que a taxa de variação é nesse intervalo.
Em seguida, a temperatura aumenta até alcançar a temperatura em que será utilizada. Podemos dizer que a taxa de variação da temperatura é positiva e aproximadamente constante.
Por fim, alcançamos a temperatura de uso e seu valor permanece constante. Então podemos dizer que a sua taxa de variação volta a ser .
Resumidamente:
Parte 1: ;
Parte 2: ;
Parte 3: .
Partiu último item!
Passo 4
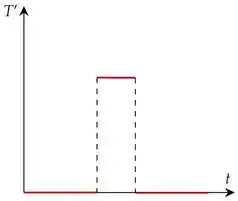
Por fim, o item (c) pede pra usarmos as informações anteriores pra esboçarmos o gráfico de .
Vamos ver como vai ficar:

Uhuuul! Conseguimos fechar a questão!
Resposta
a)
b)
Parte 1: ;
Parte 2: ;
Parte 3: .
c)