Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.2 - Ex. 26

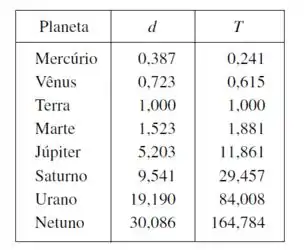
A tabela mostra as distância médias dos planetas ao Sol (tomando como unidade de medida a distância da Terra ao Sol) e seus períodos (tempo de revolução em anos).

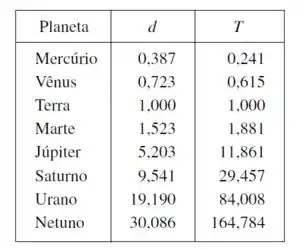
(a) Ajuste um modelo de função potência aos dados.

(b) A Terceira Lei de Kepler para o movimento planetário afirma que “O quadrado do período de revolução de um planeta é proporcional ao cubo de sua distância média ao Sol”. Seu modelo confirma a Terceira Lei de Kepler?

Passo 1

Opa, bora lá! O problema fornece uma tabela com o período de revolução de planetas e suas respesctivas distâncias com relação ao Sol.

No item (a) devemos fazer um ajuste dos dados da tabela com uma função potência do tipo

Fazendo o ajuste num programa de ajustes:

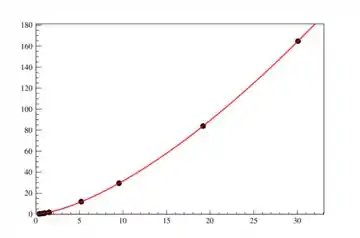
Os parâmetros do ajuste são

Passo 2

Pela Terceira Lei de Kepler, devíamos ter:

Assim, o expoente deve ser próximo de . É exatamente isso que acontece pois .

Resposta

Ajuste gráfico.
Sim, o modelo se ajusta a Terceira Lei de Kepler.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tabela mostra a média das distâncias d dos planetas ao Sol (tomando a unidade de medida para ser a distância da Terra ao Sol) e seus períodos T (tempo de revolução em anos).Ajuste um modelo de funçã

Faça um esboço do gráfico da função. Não use a calculadora. Use apenas os gráficos dados nas Figuras 3 e 13 e, se necessário, as transformações da Seção 1.3y = 0,5 x - 1

Faça um esboço do gráfico da função. Não use a calculadora. Use apenas os gráficos dados nas Figuras 3 e 13 e, se necessário, as transformações da Seção 1.3y = 4 x - 1

O tempo de meia vida do bismuto-210, Bi, é de 5 dias.a) Se uma amostra possui uma massa de 200 mg, encontre a quantidade remanescente após 15 dias.b) Encontre a quantidade remanescente após t dias.c)

Use o gráfico V da figura 11 para estimar a meia vida de uma carga viral do paciente 303 durante o primeiro mês de tratamento.