Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.4 - Ex. 31
O tempo de meia vida do bismuto-210, Bi, é de 5 dias.
a) Se uma amostra possui uma massa de 200 mg, encontre a quantidade remanescente após 15 dias.
b) Encontre a quantidade remanescente após t dias.
c) Estime a quantidade remanescente após 3 semanas.
d) Use o gráfico para estimar o tempo necessário para a massa ser reduzida a 1 mg.
Passo 1
Eaee, belezinha?? Bom... a questão nos diz que tempo de meia vida do bismuto-210, é de dias.
A partir disso, queremos encontrar a quantidade remanescente após dias se uma amostra possui uma massa de .
Também queremos encontrar a quantidade remanescente de bismuto-210 após dias e estimar a quantidade remanescente após semanas.
Por fim, devemos esboçar o gráfico para estimar o tempo necessário para a massa ser reduzida a .
Para resolvermos esses problemas, temos que saber como é a função de meia vida:
Onde:
- é a quantidade da substância no tempo ;
- é a quantidade inicial da substância;
- é o tempo de meia-vida, ou seja, o tempo necessário para a quantidade se reduzir pela metade.
Em cada letra, vamos substituir os valores nessa função e achar o que é pedido.
Agora vamos lá!! 😉
Passo 2
a) A massa da amostra é de
O tempo de meia vida é de dias. Como desejamos saber após dias, temos que ciclos de meia vida aconteceram.
Assim, basta substituir na equação:
Passo 3
b) Após dias, utilizando os mesmos dados da letra a), exceto a quantidade de dias, que queremos igual a , temos:
Passo 4
c) Agora, devemos fazer a mesma coisa para semanas ( dias):
Passo 5
d) Lembrando que a função que queremos traçar o gráfico é:
Traçando a curva de meia vida, temos que:
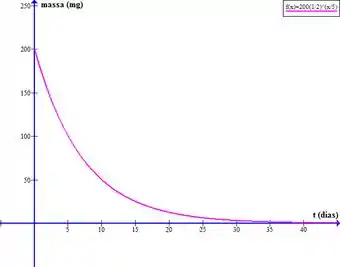
Para remanescer , usamos a função da meia vida:
Entendeu direitinho?? Responde aee 😉