A tabela mostra a média das distâncias dos planetas ao Sol (tomando a unidade de medida para ser a distância da Terra ao Sol) e seus períodos (tempo de revolução em anos).
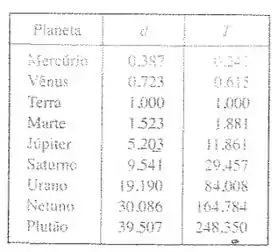
- Ajuste um modelo de função potência aos dados.
- A terceira Lei de Kepler para o movimento Planetário estabelece que “O quadrado do período da revolução de um planeta é proporcional ao cubo de sua distância média ao Sol”. Seu modelo confirma a terceira Lei de Kepler?
Passo 1
Opa, bora lá!
O enunciado nos dá a seguinte tabela
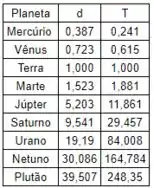
Essa tabela mostra a média das distâncias dos planetas ao Sol, a unidade de medida é o tamanho do Sol e seus períodos em anos.
A primeira coisa que ele pede pra a gente fazer é o ajuste um modelo de função potência aos dados.
E tambem a partir da função que vamos obter, temos que verificar a terceira Lei de Kepler que diz “O quadrado do período da revolução de um planeta é proporcional ao cubo de sua distância média ao Sol”. Ou seja
Onde é uma constante.
Parece complicado?
Para resolver esse problema, como a questão nos indica a usar um software, vamos primeiramente usar o excel para obter uma função potencial do tipo
Em que e são constantes que vamos descobrir.
E depois vamos verificar se é possivel verificar a terceira Lei de Kepler.
Veja só!
Passo 2
Poderíamos fazer essas contas todas a mão, mas daria um trabalho imenso e precisaríamos de conhecimentos que ainda não temos...
Como essa questão está simbolizada no livro como uma questão que temos que usar o auxílio de recursos digitais, vamos usar o Excel a nosso favor.
Passando a tabela do enunciado no Excel, criamos um gráfico de em função de e usamos a ferramenta de Linha de Tendência de Potência para obter uma aproximação do comportamento da função
Depois exibimos a função que o Excel criou e nos deparamos com isso
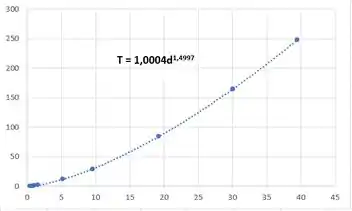
Podemos aproximar a expressão presente no gráfico para:
Tranquilo até aqui?
Passo 3
Beleza, agora na letra (b) a gente tem que analisar se esse ajuste obedece a lei de Kepler dada por:
No passo anterior encontramos que
Como na terceira Lei de Kepler temos vamos elevar os dois lados ao quadrado...
Usando as propriedades de potências, temos que , ou seja
Comparando com , vemos que como é uma constante, podemos confirmar que a Terceira Lei de Kepler é satisfeita e .
E aí! Entendeu tudo? Responde Aí!
Resposta
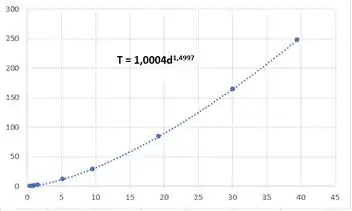
Obedece a lei de Kepler