Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.3 - Ex. 48
A tank contains 1000 L of pure water. Brine that contains 0.05 kg of salt per liter of water enters the tank at a rate of 5 Lymin. Brine that contains 0.04 kg of salt per liter of water enters the tank at a rate of 10 Lymin. The solution is kept thoroughly mixed and drains from the tank at a rate of 15 Lymin. How much salt is in the tank (a) after t minutes and (b) after one hour?
Passo 1
Muito parecido com a questão anterior. Sendo que agora temos duas entradas de agua. Então temos um tanque com agua pura, entra 15 L/min e sai 15 L/m. Podemos desenhar assim o nosso tanque.
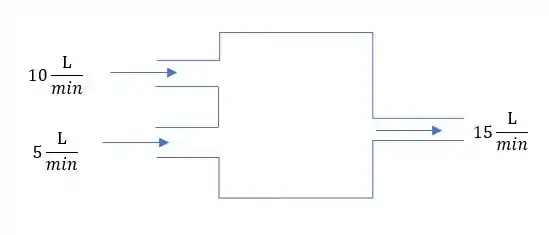
Então temos que escrever essa equação diferencial dessa Massa de SAL
Nós não sabemos como se comporta a mistura de Sal dentro do tanque então deixamos como função de m.
Prontinho, agora sim podemos calcular
Passo 2
Agora vamos integrar em ambos os lados
Prontinho. Conseguimos descrever como funciona nossa massa de sal se mistura no tanque. Temos também dados de contorno que nos ajudam a achar C
Logo podemos escrever nossa função como
Passo 3
Entao depois t minutos teremos
E após 60 minutos
Então terminamos por aqui. Te vejo na próxima resolução
: )