Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 47
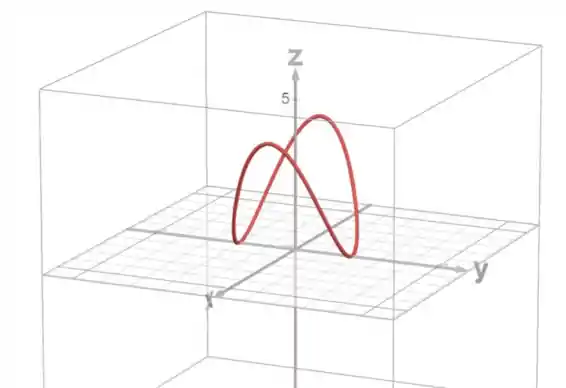
Tente esboçar à mão a curva obtida pela intersecção do cilindro circular com o cilindro parabólico . Determine então as equações paramétricas dessa curva e utilize um computador para desenhá-la.
Passo 1
Beleza, galera? Primeiro, vamos tentar determinar as equações paramétricas da curva.
Se estamos falando de intersecção, então devemos achar equações paramétricas que possam satisfazer as equações das duas superfícies.
A gente vai começar parametrizando o cilindro circular, depois a gente vai utilizar a parametrização encontrada no cilindro circular, no cilindro parabólico e assim teremos as variáveis parametrizadas.
Podemos parametrizar um cilindro circular com:
E
Para desenhar a intersecção, iremos utilizar o GeoGebra.
Passo 2
Vamos começar com o cilindro circular:
Uma boa parametrização pra esse cilindro é:
Agora, para o cilindro parabólico, devemos ter:
Então, as equações paramétricas da curva de intersecção serão:
Agora, vamos utilizar um computador pra desenhar as duas superfícies e termos uma ideia de como é a curva de intersecção entre elas:
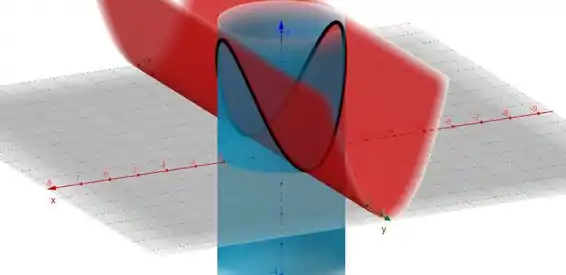
E utilizando as equações paramétricas já encontradas, vamos efetivamente desenhar a curva, beleza?
