Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 1.2 - Ex. 9
Um tanque de água tem a forma de um hemisfério com raio . A água vaza por um orifício circular de no fundo plano. Use as informações do Problema 7 para obter a equação diferencial para a altura da água com relação ao tempo .
Passo 1
Aqui temos um tanque em formato de hemisfério, ou seja, metade de uma esfera. Então ele é assim olha:
A água dentro desse tanque ta vazando por aquele orifício, que tem de comprimento (lembrando que aqui é o comprimento da circunferência como um todo, e não o seu raio beleza?)
Conforme a água vai vazando pelo orifício, a altura da água dentro do tanque vai diminuindo, e vamos encontrar essa relação através da equação diferencial que envolve , beleza?
Passo 2
O enunciado nos disse pra utilizar as informações do problema 7, e lá ele fala pra gente que, considerando o atrito, o volume de água que sai do tanque por segundo é aproximadamente , ou seja:
Onde o sinal de menos quer dizer que o volume ta diminuindo, é a área do orifício, é a aceleração da gravidade e é a altura.
Mas isso aí é , como podemos fazer pra chegar no ?
Passo 3
Para manipular a expressão de e chegarmos em , vamos pensar no volume que a água ocupa dentro do tanque.
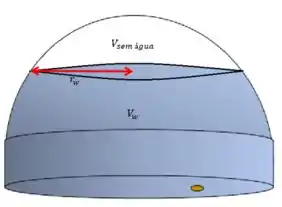
O volume que a água ocupa será dado pelo volume total do tanque (hemisfério de raio menos o volume sem água, que é o volume de um hemisfério de raio
Como estamos falando da metade de uma esfera, então o volume do hemisfério vai ser metade do volume de uma esfera:
Ok, mas quem é ? Repara que o raio da superfície da água vai mudando conforme a água vai vazando, não é? Então vamos pensar no nosso tanque de uma forma geométrica:
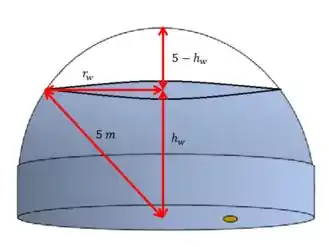
Lembrando que como temos uma metade de esfera, o raio é sempre 5.
Utilizando Pitágoras, temos que
Substituindo em :
Derivando os dois lados em relação a :
Por regra da cadeia:
Beleza, encontramos uma expressão que relaciona e , agora podemos brincar com as expressões que temos hehe
Passo 4
Pelos dados do exercício 7, temos:
E pelas manipulações que fizemos no passo 3, temos:
Substituindo em :
Boaaaa, agora é só substituir os valores :P
Passo 5
Beleza, encontramos que a expressão para a altura da água em função do tempo é
Agora vamos substituir os valores.
Temos que é a área do orifício. O raio do orifício é de .
Portanto, a área do orifício é
Passo 6
Substituindo os dados do passo 5 na expressão de :
De acordo com o exercício 7, temos
E por fim: