Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 26
O número de franquias de uma certa cadeia popular de cafeteiras é mostrada na tabela. (Esse número é obtido no dia 30 de junho de cada ano.)
a) Encontre a taxa média do crescimento.
de a de a de a .
Em cada caso, inclua as unidades.
b) Estime a taxa instantânea de crescimento em 1998 tomando a média de duas taxas médias de variação. Quais são as suas unidades?
c) Estime a taxa instantânea de crescimento em medindo a inclinação da tangente.
Passo 1
Fala aí, galerinha!
Nesse problema foi dada uma tabela de um número de lojas de uma franquia em função dos anos.
A partir dessa tabela, queremos obter a taxa de crescimento entre e , e e entre e .
Com esses resultados, temos tambem que estimar a taxa de variação instantânea em pela média das duas taxas mais próximas e pela reta tangente.
Tem ideia de como fazemos isso?
Primeiramente, para determinar a taxa de variação nos intervalos pedidos, vamos usar a formulinha
Em que é a variação do número de franquias e é a variação do tempo em anos.
Para responder o item b), vamos calcular a média da taxa de variação entre e .
Por último, para o item c), vamos esboçar os pontos no plano cartesiano e estimar o gráfico . Depois esboçamos a reta tangente em e usamos a equação para obter a inclinação...
Bora começar!
Passo 2
Vamos começar calculando as taxas de variações , e .
Fazendo a taxa, que é de a
Pela tabela, vemos que e , ou seja
Fazendo a taxa, que é de a
Substituindo os valores da tabela...
Por último, fazendo a taxa, que é de 1998 a
Pela tabela, vemos que e
Tranquilo até aqui?
Passo 3
No item b) queremos calcular a taxa de variação instantânea em a partir das médias das variações mais próximas.
Então, como as taxas mais próximas acontecem entre e , temos
Se e , então
Bacana, não é?
Passo 4
Esboçando esses pontos no plano cartesiano e ligando-os, vamos obter o gráfico de como
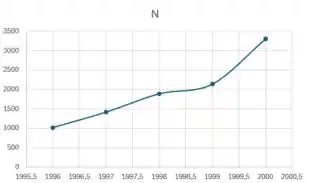
Vamos desenhar a reta tangente em
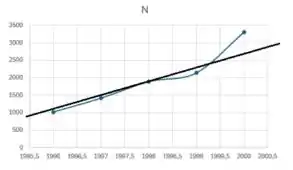
Perceba que a reta tangente passa por e , aproximadamente.
Usando a equação descrita no passo 1, podemos calcular a inclinação dessa reta e a taxa de variação instantânea em .
Veja que o resultado que obtemos nesse passo não é o mesmo do resultado do passo anterior, porém é muito próximo.
E aí! o que achou? Responde Aí!
Resposta
taxa
taxa
taxa
Taxa instantânea pela média é igual a:
Taxa instantânea pela tangente é igual a: