Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.6 - Ex. 14
Um tanque cilindro com raio de e altura de tem cheios de água. Encontre o trabalho necessário para bombear toda água por cima da borda superior do tanque.
Passo 1
Vamos usar nossa criatividade para interpretar esse problema. Queremos o trabalho para bombear toda a água para cima. Podemos cortar nosso volume de água em fatias bem fininhas e considerar que a força para mover uma fatia é constante e deve superar a força peso.
Aí lembramos que para uma força constante:
Para descobrimos o trabalho total, devemos somar o trabalho realizado em cada fatia. Vamos lá!
Passo 2
Vamos descobrir o valor da força por fatia.
Já que nossas fatias são bem finas, podemos dizer que elas têm uma altura infinitesimal e raio de . Logo, o volume delas é:
Para achar a força peso, podemos multiplicar o volume pela densidade de peso da água que é igual a . E como queremos que a força por fatia supere a força peso:
Passo 3
Precisamos entender agora como é o nosso valor de para cada fatia:
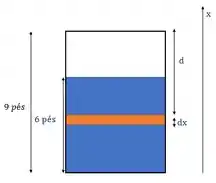
Repara que podemos escrever:
Sendo que vai de a .
Passo 4
O trabalho fica com essa carinha:
Mas queremos o trabalho total. Lembra que integrar também é calcular somatório: