Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.5 - Ex. 9
9. A tarifa T cobrada para dirigir em um certo trecho de uma rodovia com pedágio é de $ 5, exceto durante o horário de pico (entre 7 da manhã e 10 da manhã e entre 4 da tarde e 7 da noite), quando a tarifa é de $ 7.(a) Esboce um gráfico de T como função do tempo t, medido em horas após a meia-noite.(b) Discuta as descontinuidades da função e seu significado para alguém que use a rodovia.
Passo 1
Bora lá! De acordo com o enunciado, o pedágio em um trecho rodoviário tem o custo de em todos os horários, exceto no horário de pico, quando o preço é de .
Com base nisso, temos que em criar um gráfico que relacione a tarifa com o tempo em horas, considerando meia noite como o horário inicial. Depois, iremos analisar o gráfico e discutir suas descontinuidades.
Para simplificar, podemos dividir as 24 horas do dia em alguns intervalos. O horário de pico inicia às 7 da manhã, encerra às 10, recomeça às 4 da tarde (16h) e termina novamente às 7 da noite (19h). Resumindo:
- De h até h: A tarifa é
- De h até h: A tarifa é
- De h até h: A tarifa é
- De h até h: A tarifa é
- De h até h: A tarifa é
Passo 2
Vamos considerar que o preço da tarifa muda exatamente no momento que a hora vira, por exemplo, as a tarifa é e as a tarifa é . Podemos escrever isso em forma de função:
Fazendo um gráfico, temos:
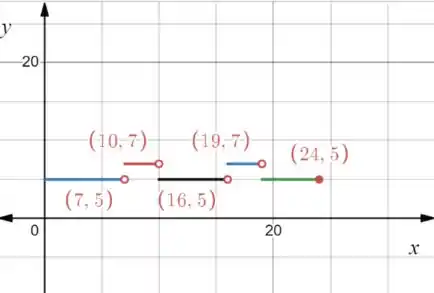
Passo 3
Na prática, a descontinuidade da função em e significa uma mudança repentina no preço do pedágio. Isso significa que se o motorista quiser pagar mais barato ele deve evitar entrar na rodovia em horários próximos a e , quando os preços ficam mais altos.
Resposta
(a)
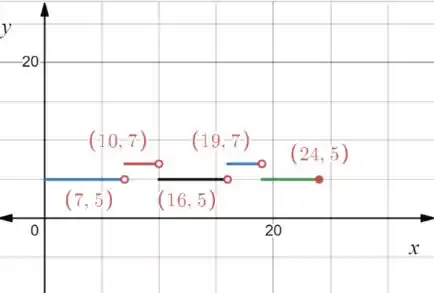
(b) Se o motorista quiser pagar mais barato ele deve evitar entrar na rodovia em horários próximos a e , quando os preços ficam mais altos.