46-Seja a função cujo gráfico está mostrado no Exercício 2. Para cada intervalo, determine (i) se está satisfeita a hipótese do Teorema do Valor Intermediário e (ii) se está satisfeita a conclusão desse mesmo teorema.
a)
b)
c)
Passo 1
Genteee, a primeira coisa que nós temos que fazer é lembrar a hipótese e a conclusão do Teorema do Valor Intermediário.
Hipótese: tem que ser uma função contínua em um intervalo fechado e um número entre e .
Conclusão: Existe no mínimo um no intervalo , tal que .
Agora, precisamos de uma coisa fundamental para resolvermos a questão, o gráfico do exercício 2 né ?!
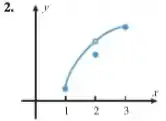
Pronto, já temos todas as ferramentas para fazermos a questão, então vamos lá !
Passo 2
a)Galera, como temos uma bolinha aberta no 2, isso quer dizer que a função não é contínua no 2, portanto a hipótese do teorema não é satisfeita. No entanto, nós temos um valor para , então a conclusão é satisfeita. Eu acho que fica mais claro se nós pensarmos na função como algo assim:
Sacou ??? A função de fato não é contínua para , mas ela tem um valor definido nesse ponto, o que faz com que a hipótese não seja satisfeita mas a conclusão sim.
Passo 3
b) Galera, como temos uma bolinha aberta no 2, isso quer dizer que a função não é contínua no intervalo fechado , portanto a hipótese do teorema não é satisfeita. No entanto, nós temos um valor para , então a conclusão é satisfeita.
Passo 4
c) Galera, como temos uma bolinha aberta no 2, isso quer dizer que a função não é contínua no intervalo fechado , portanto a hipótese do teorema não é satisfeita. No entanto, nós temos um valor para , então a conclusão é satisfeita.
Amiguíneos, vocês podem estar pensando: Nossa que questão tosca, para todos os itens a hipótese não foi satisfeita e a conclusão. Caraaa, mas eu já vou te falando que esse exercício chama atenção para algo impontante, então, atenção:
Olha só, você podia ler esse teorema muito rapidamente,em um dia de Sol à beira da piscina (onde, talvez, todos nós quiséssemos estar agora hahahh), e pensar que se a hipótese do teorema não fosse satisfeita a conclusão, automaticamente, não seria. No nosso caso, se a hipótese do teorema for atendida a conclusão automaticamente vai ser atendida, mas se isso não ocorrer nada impede que a conclusão seja satisfeita, sacou a diferença ??? Ainda podemos falar mais, se o não estivesse definido a conclusão do teorema para o intervalo não seria satisfeita.
Resposta
a)Satisfaz a conclusão, mas não a hipótese.
b) Satisfaz a conclusão, mas não a hipótese.
c) Satisfaz a conclusão, mas não a hipótese.