Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.2 - Ex. 38
A tensão em cada extremidade da corrente tem um módulo de N. Qual o peso da corrente?
Passo 1
Nessa questão nós temos duas tensões e precisamos calcular o peso da corrente para que o sistema fique em equilíbrio. Ou seja, para que o somatório das forças em e em seja igual a . Vamos desenhar todas nossas forças em um sistema cartesiano:
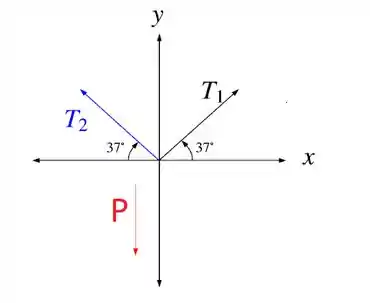
Perceba que o somatório das forças em não nos ajudará em nada, pois as componentes de e se cancelarão. Por isso, vamos ver o que acontece no eixo :
Como o problema nos disse que aa tensão em cada extremidade da corrente tem módulo igual a , então:
Resposta
34.
Exercícios de Livros Relacionados
Sabendo que u → = 2 ,v → = 3eu → . v → = - 1 , calcular: u → - 3 v → . u →
Sabendo que u → = 2 ,v → = 3eu → . v → = - 1 , calcular: u → + v → . ( v → - 4 u → )
Sabendo que u → = 2 ,v → = 3eu → . v → = - 1 , calcular: 2 v → - u → . 2 v →
Os pontos A ,BeC são vértices de um triângulo equilátero cujo lado mede 20c m . Calcular A B - .A C - e A B - .C A - .
Calcular u → . v → + u → . w → + v → . w → , sabendo que u → + v → + w → = 0 , u → = 2 , v → = 3 e w → = 5 .