Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.8 - Ex. 3
Passo 1
Fala galerinha tranquilidade, nessa bateria de exercícios nós iremos calcular os pontos extremos com base nas restrições de cada um dos casos, para isso temos que obedecer a seguinte regra:
Podemos calcular cada um dos gradientes:
Obtendo os gradientes podemos utilizar a igualdade:
Passo 2
Conhecendo a igualdade dos gradientes e do multiplicador de lagrange podemos calcular o valor do multiplicador e de x:
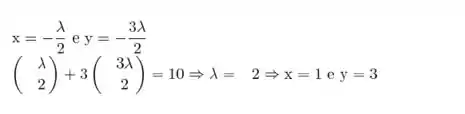
Passo 3
Agora consideramos as restrições da reta, que são um pouco diferentes de casos circulares o ponto de extremo é:
(1,3)
Resposta
O valor extremo é:
