Uma tigela tem a forma de um hemisfério com diâmetro de . Uma bola pesada com diâmetro de é colocada dentro da tigela, e depois despeja-se água até uma profundidade de centímetros. Encontre o volume de água na tigela.
Passo 1
Nesse problema uma bola dentro de uma tigela com água. Queremos saber o volume de água dentro dessa tigela!
Nós consideraremos dois casos, um em que a bola não é completamente submersa, e outro, em que é. Com as informações dadas faremos os seguintes diagramas:
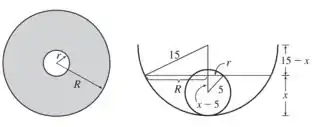
Passo 2
Caso 1: a bola não é completamente mergulhada, então a altura varia em . A seção transversal de água paralela à superfície será a área sombreada do primeiro diagrama. Nós podemos encontrar a área da seção transversal de altura acima do fundo do arco usando o Teorema de Pitágoras:
Com isso, temos a seguinte área:
Assim, o volume de água com profundidade é:
Passo 3
Caso 2: Neste caso, podemos encontrar o volume simplesmente subtraindo o volume deslocado pela bola do volume total dentro da tigela sob a superfície da água. O volume total sob a superfície é apenas o volume de uma tampa da tigela, então usamos a fórmula do exercício 49 para nossa resolução:
O volume da bola é:
Assim, o volume total é:
Prontinho!
Resposta
Com a bola não completamente submersa, .
Com a bola completamente submersa, .