Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.2 - Ex. 67

Encontre o volume comum a duas esferas, cada uma com raio r , se o centro de cada esfera estiver na superfície da outra esfera.

Passo 1

Primeiramente vamos desenhar a situação do problema para ficar mais claro que está acontecendo. Temos, então

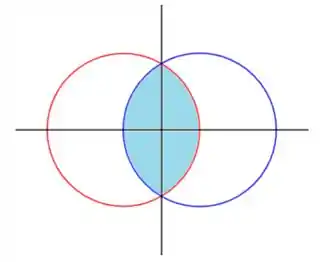
Onde o círculo vermelho tem centro - r 2 , 0 e sua equação é dada por

x + r 2 2 + y 2 = r 2

Enquanto que o círculo azul tem centro r 2 , 0 e sua equação vai ser dada por

x - r 2 2 + y 2 = r 2

Pela simetria temos que o volume da região da esquerda em torno do eixo x e o volume da região da direita em torno do eixo x são iguais. Então, o volume total é dado por V = 2 V 1 onde V 1 será dado por

V 1 = ∫ 0 r 2 π y 2 d x = ∫ 0 r 2 π ⋅ r 2 - x + r 2 2   d x

V 1 = ∫ 0 r 2 π ⋅ r 2 d x - ∫ 0 r 2 π ⋅ x + r 2 2 d x = π r 3 2 - 7 π r 3 24 = 12 π r 3 - 7 π r 3 24 = 5 π r 3 24

Sendo assim, nosso volume total será dado por

V = 2 V 1 = 5 π r 3 12

Resposta

5 π r 3 12

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume do sólido descrito por S . A base de S é um disco circular com raio r . Seções transversais paralelas perpendiculares à base são quadrados.
Encontre o volume do sólido descrito por S . O sólido S é delimitado por círculos que são perpendiculares ao eixo x , cruzam o eixo x e têm centros na parábola y = 1 2 ⋅ 1 - x 2 , - 1 ≤ x ≤ 1 .
Uma tigela tem a forma de um hemisfério com 30c m de diâmetro. Uma bola pesada com 10c m de diâmetro é colocada na tigela e a água é derramada na tigela a uma profundidade de h centímetros. Encontre o
Encontre o volume do sólido descrito por S . A base de S é a região delimitada por y = 2 - x 2 e o eixo x . As seções transversais perpendiculares ao eixo y são quartos de círculo.
Use camadas cilíndricas para encontrar o volume do sólido que é gerado quando a região envolvida por y = 1 / x 3 , x = 1 ,x = 2ey = 0 gira em torno da reta x = - 1 .